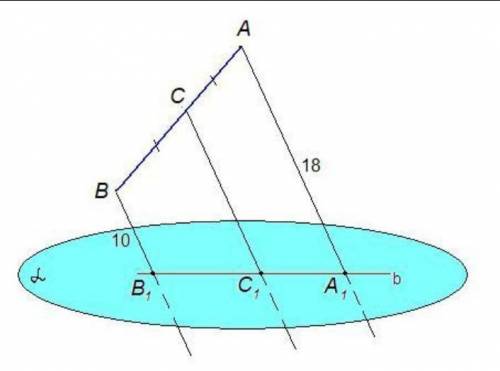
Через концы отрезка АВ и его середину С проведены параллельные прямые, которые пересекают некоторую плоскость α в точках А₁, В₁ и С₁ соответственно. Найти длину отрезка СС₁, если отрезок АВ не пересекает плоскость α и АА₁ = 18 см, ВВ₁ = 10 см.
14 см
Объяснение:
Параллельные прямые АА₁ и ВВ₁ задают плоскость, в которой лежит отрезок АВ и точка С, лежащая на нем.
В этой плоскости через точку С можно провести единственную прямую, параллельную АА₁, значит прямая СС₁ так же лежит в этой плоскости.
Плоскость (АВВ₁) пересекает плоскость α по прямой b, на которой лежат точки А₁, В₁ и С₁.
Итак, четырехугольник ABB₁A₁ - трапеция с основаниями АА₁ и ВВ₁.
СС₁ - средняя линия трапеции, а значит, равна полусумме оснований:
CC_1=\dfrac{AA_1+BB_1}{2}=\dfrac{18+10}{2}=\dfrac{28}{2}=14CC
1
=
2
AA
1
+BB
1
=
2
18+10
=
2
28
=14 см
ответ: 3 прямоугольника со сторонами
а) 2 и 18
б)3 и 12
в) 4 и 9
Найдите периметр каждого из них:
р=(a=b)*2
а) (2+18)*2=20*2=40 см
б) (3+12)*2=15*2=30 см
в) (4+9)*2=13*2=26 см
2) найти длину стороны равностороннего треугольника, периметр которого равен периметру одного из этих прямоугольников в ответе на вышеуказанный вопрос
Равносторонний треугольник - это треугольник, у которого все стороны равны. Следовательно, 30 см:3=10 см сторона равностороннего треугольника