Пошаговое объяснение:
здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности
1 страшная формула - это однополостный гиперболоид
две других - это плоскости
объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:
, где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.
плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу
запишем наш эллипс
теперь нам надо каноническое уравнение нашего эллипса
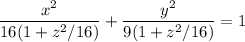
упростим
площадь этого замечательного гиперболоида вычисляется по формуле
S=πab
у нас
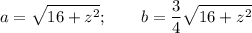
отсюда
S=π*(3/4)(16+z²)
вот, собственно, и все "загогулины"
остался только объем
Составить уравнение линии,каждая точка которой отстоит от прямой x=8 на расстояние в 2 раза больше,чем от точки A(-1; 7).
Пусть точка М(х; у) удовлетворяет заданным условиям.
Расстояние от точки М до А равно: АМ = √(х - (-1))² + (у - 7)²).
Расстояние точки М от прямой х = 8 равно (8 - х).
По условию задания 2*√((х - (-1))² + (у - 7)²) = (8 - х).
Возведём обе части уравнения в квадрат.
4*((х + 1))² + (у - 7)²) = (8 - х)². Раскроем скобки.
4*(х² + 2х + 1 + у² - 14у + 49) = 64 - 16х + х²,
4х² + 8х + 4 + 4у² - 56у + 196 = 64 - 16х + х²,
3х² + 4у² + 24х - 56у + 136 = 0.
Выделяем полные квадраты:
для x:
3(x²+2·4x + 42) -3·42 = 3(x+4)²-48
для y:
4(y²-2·7y + 72) -4·72 = 4(y-7)²-196
В итоге получаем:
3(x + 4)² + 4(y - 7)² = 108 .
Разделим все выражение на 108
( (x + 4)²/36) + ((y - 7)²/27) = 1.
Получили каноническое уравнение эллипса:
( (x + 4)²/6²) + ((y - 7)²/(3√3)²) = 1.
4. Параметры кривой.
Полуоси эллипса равны: a = 6, b = 3√3.
Центр эллипса расположен в точке: C(-4; 7) .
Найдем координаты фокусов F2(-c;0) и F1(c + x(C);0+y(C)), где c - половина расстояния между фокусами /
c = √(a² - b²) = √(36 - 27) = √9 = 3.
Итак, c учетом центра, координаты фокусов равны:
F2(-3+(-4;0+7) = (-7; 7),
F1(3+(-4);0+7) = (-1; 7) = A.
Тогда эксцентриситет будет равен: e = c/a = 3/6 = 1/2.
Вследствие неравенства c < a эксцентриситет эллипса меньше 1.