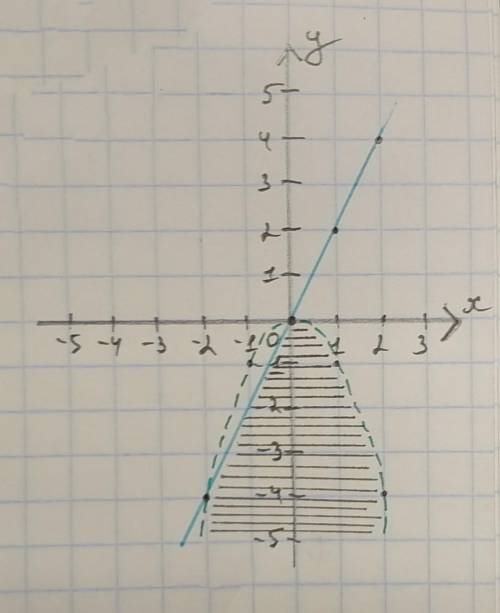
Решение во вложении.
Для решения неравенства грфически вам нужно преобразовать его в функцию f(x)=(...), построить графики данных уравнений, а затем определить, в какой из плоскостей, ограничиваемых графиком, находится нужное множество решений. Для прямой - слева или справа, для параболы - внутри неё или снаружи. Для этого берём любую точку из перечисленных областей и подставляем в неравенство. Если оно верное, зашриховываем выбранную зону. Если нет - противоположную ей область. Для прямой это оказалась область справа от неё, а для параболы - внутри. Затем ищем пересечение штриховок. Это ответ.
Обратите внимание: графическим решением неравенства при строгом знаке (> или <) является ТОЛЬКО определённая вами область, высекаемая графиком. Если знаки нестрогие (<= или >=), то точки самого графика тоже принадлежат множеству решений системы.
Обращаю внимание: я нарисовала новый чертёж с ответом отдельно. Это делать необязательно, достаточно просто хорошо прорисовать область решений на первом чертеже.

32 см.
Пошаговое объяснение:
Пусть АВ=ВС=5х см, АС=6х см
В равнобедренном треугольнике высота является и медианой.
АН=СН=3х см.
По теореме Пифагора ВС²=ВН²+СН²
(5х)²=8²+(3х)²; 25х²=64+9х²; 16х²=64; х²=4; х=2.
АВ=ВС=5*2=10 см4 АС=6*2=12 см
Р=10+10+12=32 см.