1) Велосипедист едет в обратном направлении со скоростью 12 км/ч.
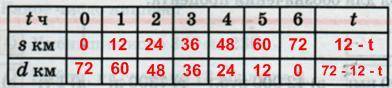
2) Заполним таблицуЕсли велосипедист еще не выехал из березовки, то до Москвы 72 км.
Если велосипедист проехал 1 ч со скоростью 12 км/ч, то есть 12 км, то до Москвы еще осталось 72 − 12 = 60 км.
Если он проехал 2 ч с той же скоростью, то есть 2 * 12 = 24 км, то до Москвы осталось 72 − 24 = 48 км, и далее:
при t = 3:
s = 3 * 12 = 36;
d = 72 − 36 = 36.
при t = 4:
s = 4 * 12 = 48;
d = 72 − 48 = 24.
при t = 5:
s = 5 * 12 = 60;
d = 72 − 60 = 12.
при t = 6:
s = 6 * 12 = 72;
d = 72 − 72 = 0.
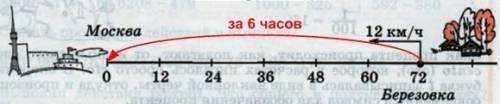
3) Покажем движение по числовому лучу:
1)Множество натуральных чисел
Множество натуральных чисел - определение
Множество натуральных чисел включает в себя все целые числа больше нуля — положительные целые числа.
Например: 1, 3, 20, 3057. Множество не включает в себя цифру 0.
Множество целых чисел
Множество целых чисел - определение
В это числовое множество входят все целые числа больше и меньше нуля, а так же ноль.
Например: -15, 0, 139.
2) Основой такого доказательства служат приводимые ниже определения
подмножества и пустого множества (курсив и полужирный шрифт везде мои):
1. Множество А называется подмножеством множества В, если все элементы,
из которых состоит А, входят и в В. Это соотношение символически обозначается
так: А < В (или А L В; извините, но правильных знаков в Спецсим-ах я не нашёл)
2. Множество, не содержащее ни одного элемента, называется пустым
и обозначается символом Ǿ (или обычным нулём: 0).
Совершенно очевидно, что в первом определении речь идёт о двух непустых
множествах, поскольку в каждом предполагается наличие элементов, которые
и сравниваются между собой.
3) (Ток не спутай,В другую сторону их писать надо)Э-простая,и Э зачёркнутая.
97
Пошаговое объяснение:
В начале любого числа стоит ненулевая цифра. Пусть первая цифра равна 1. Тогда сумма цифр в числе равна 1 + 2 + 3 + 9 = 15. Чтобы сумма цифр стала равна 16, нужно все доступные разряды заменить на нули, но один из них заменить на единицу. Так как из 100 цифр занято 4, то существует разместить единицу среди оставшихся разрядов.
Пусть первая цифра равна 2. Тогда сумма цифр уже равна 16, все оставшиеся разряды возможно заменить только нулями. Получаем ещё одно подходящее число.
Если же первая цифра больше 2, то сумма цифр будет больше 16, эти варианты заведомо не подходят.
Итого 97 подходящих чисел.