Question

1. Определить координаты точки пересечения графически. а) y = 2x - 4 и у = 1 - 2х б) у = 3х и у = 2 - х в) у = х и х = 4 2. Выделение квадарата бинома. а) х^2 - 4х + 6 б) х^2 + 3х - 1 в) 2х^2 - 6х - 1 г) 2х^2 - 5х - 3

Answer 1

1)

а. (1.25;-1.5)

б. (0.5;1.5)

в. (4;4)

2)

а.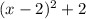 $(x-2)^2+2$

б.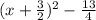$(x+ \frac 3 2)^2- \frac {13}4$

в.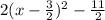$2(x-\frac32)^2-\frac{11}2$

г.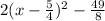$2(x-\frac54)^2-\frac{49}8$

Пошаговое объяснение:

1)

а.

Таблица для y = 2x - 4

(x;y):

(0;-4)(1;-2)

Таблица для y = 1 - 2х

(x;y):

(0;1)(1;-1)

б.

Таблица для y = 3х

(x;y):

(0;0)(1;3)

Таблица для у = 2 - х

(x;y):

(0;2)(1;1)

в.

Таблица для у = х

(x;y):

(0;0)(1;1)

Таблица для x = 4

(x;y):

(4;2)(4;1)

2)

а.

$x^2 - 4x + 6=x-2*2-x+6=x^2-2*2*x+4-4+6=(x-2)^2+6-4=(x-2)^2+2$

б.

$x^2+3x-1=x^2+x* \frac 3 2*x-1=x^2+x* \frac 3 2*x + \frac 9 4- \frac 9 4-1=(x+\frac 3 2)^2-(\frac 9 4 + \frac 4 4)=(x+ \frac 3 2)^2- \frac {13}4$

в.

$2x^2 - 6x - 1=2(x^2-3x-\frac12)=2(x^2-2*\frac32*x+\frac94-\frac94-\frac24)=2((x-\fra32)^2-\frac{11}4)=2(x-\frac32)^2-\frac{11}2$

г.

$2x^2-5x-3=2(x^2-2*\frac54x-\frac32)=x(x^2-2*\frac54x+\frac{25}{16}-\frac{25}{16}-\frac32=2(x-\frac54)^2-\frac{49}8$