
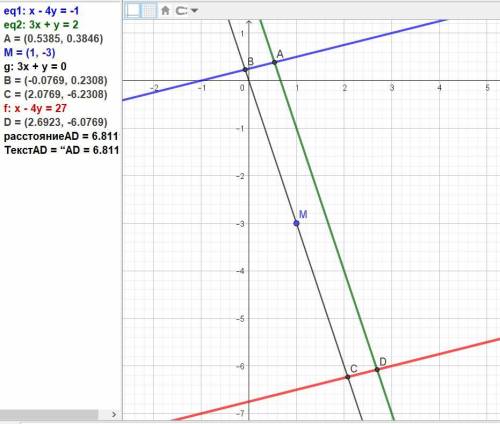
Уравнение прямой, включающей сторону ВС, найдём, подставив координаты точки М в уравнение с координатами переменных, как у параллельной прямой AD 3x + y – 2 = 0.
3*1 + (-3) + C = 0, отсюда С = -3 + 3 = 0.
Получаем уравнение BC: 3x + y = 0.
Находим вершину B параллелограмма как точку пересечения прямых АВ и ВС, решив систему:
{x – 4y + 1 = 0 x – 4y + 1 = 0
{3x + y = 0 (x4) = 12x + 4y = 0
13x + 1 = 0, x = -1/13,
y = – 3x = – 3(-1/13) = 3/13. Точка В((-1/13); (3/13)).
Находим точку С как симметричную точке В относительно точки М(1; -3).
х(С) = 2х(М) – х(В) = 2*1 - (-1/13) = 27/13,
y(С) = 2y(М) – y(В) = 2*(-3) - (3/13) = -81/13.
Уравнение прямой, включающей сторону CD, найдём, подставив координаты точки C в уравнение с координатами переменных, как у параллельной прямой AB x - 4y + 1 = 0.
(27/13) - 4(-81/13) + C = 0, отсюда С = (-27/13) – (324/13) = -351/13 = -27.
Получаем уравнение CD: x - 4y - 27 = 0.
1) d. a=50°
2) a. a=60°
3) e. a=70°
Пошаговое объяснение:
1) Проведем через точку B прямую параллельную a (и b)
Углы GAB и ABH - Односторонние. Их сумма равна 180 ⇒ ∠ABH = 180°-120°=60°
Углы FDB и DBH - Односторонние. Их сумма равна 180 ⇒ ∠FDB = 180°-(70° + 60°) = 50°
2) Проведем через точку E прямую параллельную a (и b)
Углы BCG и FEC - Соответственные. Они равны т.е ∠FEC = 40°
Углы ADE и DEF - Односторонние. Их сумма равна 180 ⇒ ∠DEF = 180°-160°=20°
∠DEC = ∠DEF + ∠FEC = 20° + 40° = 60°
3) Проведем через точку E прямую параллельную a (и b)
Углы DAE и AEF - Односторонние. Их сумма равна 180 ⇒ ∠AEF = 180°-130°=50°
Углы CBE и BEF - Односторонние. Их сумма равна 180 ⇒ ∠BEF = 180°-160°= 20°
∠BEA = ∠AEF + ∠BEF = 50° + 20° = 70°
============
Не забывайте сказать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"
Бодрого настроения и добра!
Успехов в учебе!