Это линия называется астроидой, её уравнение в параметрическом виде
таково: .
Фигура замкнута и симметрична относительно осей координат. Поэтому будем находить площадь четвёртой части фигуры, а затем полученное значение умножим на 4 .
При изменении переменной "х" от 0 до 10: , параметр t изменяется от П/2 до 0: Действительно, в 1 четверти :
Всего 39 литров (в баке мы можем получать только числа делящиеся на 3, либо те, что у нас уже есть: x было в баке, долили 2x, получим 3x)
рассмотрим случай 39 на предыдущем ходу должны быть баки 13 и 26 (что невозможно, не делятся на 3)
38 и 37 не делятся на 3, поэтому такое количество нельзя получить
рассмотрим случай 36: из 4 в 3: 1 2 12 0 12 12 из 5 в 6: 1 2 12 0 0 24 из 6 в 3: 1 2 36 0 0 0
можно получить, это и будет максимальное значение
ответ: 36 литров
решение для условия, если в бак можно налить столько,сколько в нем есть: кроме 1, мы можем получать только четное натуральное число литров (из условия следует)
Всего литров 1 + 2 + 4 + 8 + 12 + 12 = 39
1) рассмотрим случаи 39, 37, 35, 33 столько мы не можем получить, потому что оно нечетно
2) случай 38 литров:
чтобы столько получить, надо чтобы на предыдущем ходу было 2 бака по 19 литров - это невозможно, т.к. 19 - нечетное
3) случай 36 литров:
чтобы столько получить, надо чтобы на предыдущем ходу было 2 бака по 18 литров, а на ходу до этого 4 бака по 9 литров - это невозможно, т.к. 9 - нечетное
4) случай 34 литра чтобы столько получить, надо чтобы на предыдущем ходу было 2 бака по 17 литров - это невозможно, т.к. 17 - нечетное
5) случай 32 литра:
из 12 переливаем в 1 2 2 4 8 12 11 из первого во второй 0 4 4 8 12 11 из второго в третий 0 0 8 8 12 11 из третьего в четвертый 0 0 0 16 12 11 из пятого в шестой 0 0 0 16 1 22 из шестого в четвертый 0 0 0 32 1 6
значит 32 можно получить и оно наибольшее
ответ: 32 литра
(вообще для общего случая ответом является наибольшее число, меньшее чем количество баков, которое является степенью двойки)
ответ: 36 литров будет в 6 баке: 1 операция: переливаем из 3 бака 4 литра во 2 бак, в 3 баке ничего не остается, во втором становится 2 + 4 = 6 литров; 2 операция: переливаем из 5 бака во 2 бак 12 литров, в 5 баке ничего не остается, во втором становится 6 + 12 = 18 литров; 3 операция: переливаем из 4 бака в 1 бак 2 литра, в 4 баке остается 8 - 2 = 6 литров, а в первом баке становится 1 + 2 = 3 литра; 4 операция: переливаем из 4 бака в 1 бак оставшиеся 6 литров, в 4 баке ничего не остается, а в первом баке становится 3 + 6 = 9 литров; 5 операция: переливаем из 2 бака 18 литров в 1 бак, во 2 баке ничего не остается, а в 1 становится 9 + 18 = 27 литров; 6 операция: переливаем из 1 бака в 6 бак 24 литра, в первом остается 27 - 24 = 3 литра, а в 6 становится 12 + 24 = 36 литров.
Это линия называется астроидой, её уравнение в параметрическом виде
таково: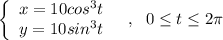 .
.
Фигура замкнута и симметрична относительно осей координат. Поэтому будем находить площадь четвёртой части фигуры, а затем полученное значение умножим на 4 .
При изменении переменной "х" от 0 до 10: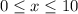 , параметр t изменяется от П/2 до 0:
, параметр t изменяется от П/2 до 0: 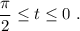 Действительно, в 1 четверти :
Действительно, в 1 четверти :