Математика: 1) Какая цифра в числе 100101102103... стоит на 91-м м

1) Какая цифра в числе 100101102103... стоит на 91-м м

👇

Ответ:

Назерке2707

07.03.2022

Тут дан ряд цифр, которые представляют из себя числа 100, 101, 102 и т.д. Необходимо узнать цифру на 91-й позиции, поскольку число нечетное и не кратно трём, значит это первая цифра числа. Так как позиция цифры 91-я, значит мы никак не выйдем за пределы первой сотни. Значит искомая цифра - 1.

4,6(37 оценок)

Открыть все ответы

Ответ:

artemsuraaye

07.03.2022

Приступим к уроку мат. анализа

a) Для поиска вертикальных асимптот нужно рассмотреть односторонние пределы в окрестностях несуществования функции

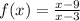
$f(x)=\frac{x-9}{x-3}$

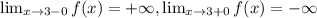
$\lim_{x \to 3-0} f(x)=+\infty, \lim_{x \to 3+0} f(x)=-\infty$

x=3 - вертикальная асимптота

$]\lim_{x \to 9-0} f(x)=-\infty, \lim_{x \to 9+0} f(x)=+\infty$

x=9 - вертикальная асимптота

ответ: 12

б) 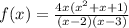$f(x)=\frac{4x(x^2+x+1)}{(x-2)(x-3)}$

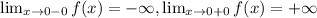
$\lim_{x \to 0-0} f(x)=-\infty, \lim_{x \to 0+0} f(x)=+\infty$

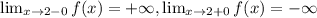
$\lim_{x \to 2-0} f(x)=+\infty, \lim_{x \to 2+0} f(x)=-\infty$

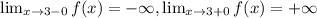
$\lim_{x \to 3-0} f(x)=-\infty, \lim_{x \to 3+0} f(x)=+\infty$

x=0, x=2, x=3 - вертикальные асимптоты

ответ: 5

________________________________________________________________________

2) $\sqrt[9]{x+1}=1+\frac{1}{9}x+\frac{\frac{1}{9}(\frac{1}{9}-1)}{2}x^2$

$\sqrt[9]{1+0,4}=1+1/9-(4/81)*0,4^2=2099/2025\approx1,037$

________________________________________________________________________

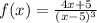
3) $f(x)=\frac{4x+5}{(x-5)^3}$

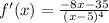
$f'(x)=\frac{-8x-35}{(x-5)^4}$

x=-35/8

При переходе через эту точку производная меняет свой знак c + на -, т.е. это точка локального максимума

ответ: -4,375

________________________________________________________________________

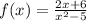
4) $f(x)=\frac{2x+6}{x^2-5}$

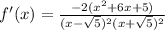
$f'(x)=\frac{-2(x^2+6x+5)}{(x-\sqrt{5})^2(x+\sqrt{5})^2}$

критические точки = x=-√5, x=√5, x=-1, x=-5

производная меняет свой знак с - на + в точке x=-5 - точка лок. минимума

ответ: -5

________________________________________________________________________

а) Найдем точки пересечения

6x-4=x²+5x-6

x²-x-2=0

x₁=-1 x₂=2

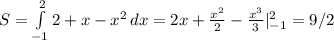
$S=\int\limits^{2}_{-1} {2+x-x^2} \, dx=2x+\frac{x^2}{2}-\frac{x^3}{3}|_{-1}^2= 9/2$

б) Точки пересечения

-x+7=x²-x+3

x²-4=0

x₁=-2, x₂=2

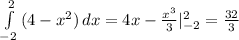
$\int\limits^2_{-2} {(4-x^2)} \, dx=4x-\frac{x^3}{3}|_{-2}^2=\frac{32}{3}$

________________________________________________________________________

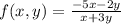
a) $f(x,y)=\frac{-5x-2y}{x+3y}$

$f_x^{'}=\frac{-13y}{(x+3y)^2}, f'_x(A)=-\frac{52}{81}$

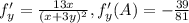
$f'_y=\frac{13x}{(x+3y)^2}, f'_y(A)=-\frac{39}{81}$

направляющий вектор {1/√10, 3/√10}

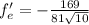
$f'_e=-\frac{169}{81\sqrt{10}}$

б) 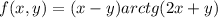f(x, y) = (x-y)arctg(2x+y)

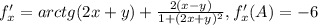
$f'_x=arctg(2x+y)+\frac{2(x-y)}{1+(2x+y)^2}, f'_x(A)=-6$

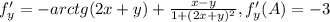
$f'_y=-arctg(2x+y)+\frac{x-y}{1+(2x+y)^2}, f'_y(A)=-3$

направляющий вектор {-2/√29, -5/√29}

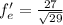
$f'_e=\frac{27}{\sqrt{29}}$

_______________________________________________________________________

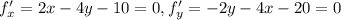
7) f'_x=2x-4y-10=0, f'_y=-2y-4x-20=0

x=-3, y=-4 - стационарная точка

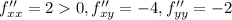
$f''_{xx}=20, f''_{xy}=-4, f''_{yy}=-2$

$\left[\begin{array}{cc}2&-4\\-4&-2\end{array}\right]=-20<0$

экстремумов нет

4,7(99 оценок)

Ответ:

studentsuka

07.03.2022

Первое, что приходит в голову при упоминании об Обломове - безвольный, бесхарактерный человек или леньтяй. Но, если взять и хорошенько подумать, то можно найти в Обломове и положительные черты.
Итак, то, что Обломов - лентяй, нет никакого сомнения. В качестве доказательства можно вспомнить его образ жизни: его нормальное положение - горизонтальное (лёжа) ; восточный, широкий халат (Восток олицетворяется сном, ленью) ; комната вся затянута паутиной; на зеркале и стёклах толстый слой пыли. Ещё одна отрицательная черта героя - это то, что он не доводил начатое дело до конца.
Всё это понятно людям, видящим только внешнюю оболочку Обломова. Самое главное, внутренний мир, они не видят. Для таких людей самое главное - работа. Им не понятны душевные волнения. Это люди типа Штольца, вездесущие и неугомонные.
Обломов жил одно время той жизнью, к которой его призывает Штольц, и, кроме разочарования, ничего больше не получил от неё. Вокруг была одна суета, а вот сути не было. Для Обломова, с детства окружённого любовью и лаской, не знавшего слова "нет", познание сути жизни было главной задачей.
Да, Обломов лентяй, но ведь не может же быть в человеке только плохих качеств. У Обломова есть самые замечательные качества любить, искренность, доброта, которые особо выделяются на фоне суеты других персонажей.
Взгляды Обломова постоянны, никто не может разрушить его идеологию. Как ни старались Ольга и Штольц, Обломов их победил.
Из всего вышесказанного я могу сделать только один вывод - нельзя точно сказать, ответить на главный вопрос: Чего в натуре обломова больше? Света или тени? Обломов слаб со стороны материальной работы, но силён духовно

4,6(100 оценок)

Это интересно:

Стиль-и-уход-за-собой

10.09.2020

Как подобрать симпатичные наряды: советы эксперта по моде...

Взаимоотношения

10.02.2023

Как привлечь внимание своего парня: 5 советов, чтобы выглядеть горячей штучкой...

Искусство-и-развлечения

26.03.2021

Как найти свой танцевальный стиль?...

Компьютеры-и-электроника