Question

При каком значении параметра "a" система линейных уравнений имеет более одного решения

Answer 1

4

Пошаговое объяснение:

Выразим из первого и второго уравнения y и z через x. Домножим первое на 5, второе на 3 и сложим:

$5(x+2y-3z)+3(3x-y+5z)=5\cdot 4+3\cdot 2\\14x+7y=26\\y=\dfrac{26}{7}-2x$

Теперь домножим второе на 2 и сложим:

$x+2y-3z+2(3x-y+5z)=4+2\cdot 2\\7x+7z=8\\z=\dfrac{8}{7}-x$

y и z линейно зависят от x, то есть на каждый найденный x приходится ровно один y и ровно один z. Значит, если подставит в третье уравнение y и z, оно должно иметь несколько решений относительно x. Также раскроем скобки и сгруппируем всё, что с х, в одной стороне, а остальное — в другой:

$4x+\dfrac{26}{7}-2x+(a^2-14)(\dfrac{8}{7}-x)=a+2\\(16-a^2)x=-\dfrac{8}{7}a^2+a+\dfrac{100}{7}$

Если 16 - a² = 0 ⇔ a = ±4:

При a = 4 0·x = 0 — бесконечно много решений, подходит.

При a = -4 0·x = -8 — решений нет, не подходит.

При всех остальных a: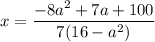 $x=\dfrac{-8a^2+7a+100}{7(16-a^2)}$

Каждый a задаёт ровно один x, что не подходит.