Пошаговое объяснение:
Остальные решаются методом интервалов.
4) (2x-1)(x+6) / (x-3) < 0
ОДЗ: x ≠ 3
Здесь три особые точки: -6, -1/2 и 3.
Берем любое число, не равное этим точкам, например, 0.
(0-1)(0+6) / (0-3) = (-1)*6 / (-3) > 0 - не подходит.
Значит, интервал, содержащий 0, (-1/2; 3) не подходит.
Зато подходят соседние интервалы.
ответ: (-6; -1/2) U (3; +oo)
5) (2x+4) / ((1-x)(2x+3)) < 0
ОДЗ: x ≠ 1; x ≠ -3/2
Переворачиваем скобку (1-x), при этом меняется знак неравенства.
2(x+2) / ((x-1)(2x+3)) > 0
Точки: -2, -3/2, 1
ответ: (-2; -3/2) U (1; +oo)
6) (x-1)(x+7)^2 / (x-3) >= 0
ОДЗ: x ≠ 3
Здесь есть особая точка -7, но, так как скобка в квадрате, то всегда положительна. Ее можно исключить.
(x - 1) / (x - 3) >= 0
ответ: (-oo; 1] U (3; +oo)
7) (2x - 9)^2 = (2x + 9)^2
Извлекаем квадратные корни слева и справа, получаем модули:
|2x - 9| = |2x + 9|
Возможны два варианта:
а) 2x - 9 = 2x + 9
-9 = 9 - это ложно, решений нет.
б) 2x - 9 = -2x - 9
4x = 0
ответ: x = 0
8) (x^2 + x - 6) / (x - 2) >= 0
ОДЗ: x ≠ 2
(x - 2)(x + 3) / (x - 2) >= 0
(x - 2) можно сократить, но, все равно x не может быть равно 2
x + 3 >= 0
x >= -3
ответ: [-3; 2) U (2; +oo)
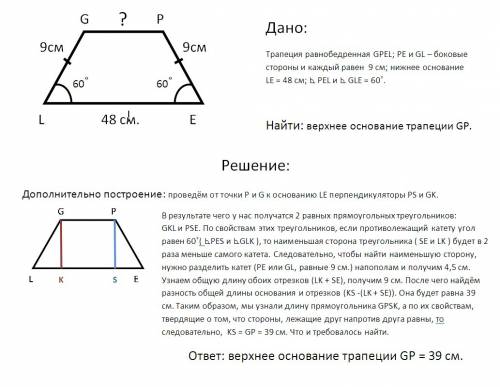
Задача решена, но без дополнительных построений ответ найти не удалось. Я всё решал кратко, поэтому объясню, как я решал задание. После построения нам требовалось лишь найти сторону получившегося прямоугольника, являвшуюся верхним основанием или частью нижнего. Верхнее нам не найти, поэтому пришлось искать нижнее основание, убрав лишние отрезки, чтобы узнать нужную сторону. Как-то так. Ладушки, мне самому пора делать уроки. Удачи! Желаю тебе когда-нибудь провести свои каникулы на этой космостанции! =)

1001.00
Пошаговое объяснение:
Все жители острова не могут быть лжецами, иначе каждый из них сказал бы правду. Возьмем некоторого рыцаря. Из его заявления вытекает, что лжецов на острове больше, чем (2001-1)/2=1000. Возьмем теперь некоторого лжеца. Его заяление ложно, поэтому кроме него не более половины жителей острова - лжецы. Это означает, что кроме него на острове не более 2000/2=1000 лжецов, т.е. вместе с ним лжецов не более 1001. Таким образом, из полученных оценок на число лжецов получаем, что единственная возможность - когда на острове ровно 1001 лжец.