84 кг
Пошаговое объяснение:
Используй пропорцию
240-100%
Х-65%
Х=(240*65):100=156кг- это сколько продали
Осталось продать 240-156=84кг
1. и) 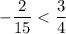 ; к)
; к) 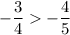 ;
; 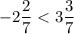 ; л)
; л) 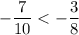
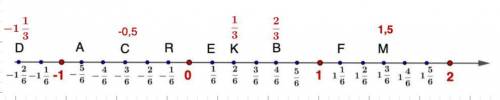
2. Точки построены. См. рисунок.
Пошаговое объяснение:
Требуется сравнить числа и записать их в виде неравенства. Также, приняв за единичный отрезок длину 6 клеток тетради, начертить координатную прямую и отметить на ней точки.
1. Сравним числа:
и)
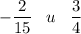
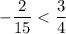
к)
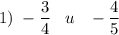
Используем основное свойство дроби:
Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, получим дробь, равную данной.Приведем дроби к общему знаменателю 20:
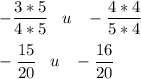
Также вспомним:
Модуль положительного числа - само число, а модуль отрицательного - число, противоположное данному.Сравним модули чисел:
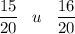
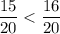
Следовательно:
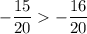 или
или 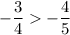
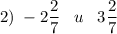
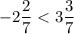
л)
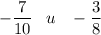
Приведем дроби к общему знаменателю 40, пользуясь основным свойством дроби:
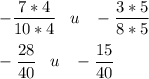
Сравним модули этих дробей:
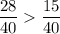
Следовательно:
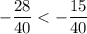 или
или 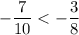
2. Начертим числовую ось и отметим единичный отрезок 6 клеток.
Если наш единичный отрезок 6 клеток, то одна клеточка будет равна одной шестой части.
Воспользуемся основным свойством дроби.
Данные дроби, у которых знаменатель отличный от 6, приведем к знаменателю 6.
Затем отметим эти числа на числовой оси.
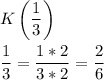
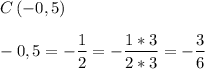
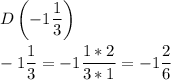
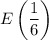
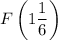
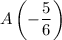
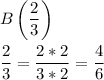
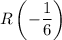
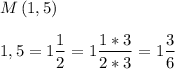
Отметим точки на числовой оси:
Пошаговое объяснение:
Пошаговое объяснение: y'²+2yy"=0; y(0)=y'(0)=1
Делаем стандартную замену y'=p(y), тогда y″=p′·p. Подставляя в уравнение, получаем p²+2y·dp/dy · p=0
Разделяя переменные, при p≠0, имеем dp/p= - dy/(2y)
Интегрируя, получаем lnp= -1/2· lny +lnC
⇒ p=C/√y ⇒ y'=C/√y , но y(0)=y'(0)=1⇒ y'(0)=C/√y(0) ⇒ С=1
Тогда если y'=C/√y ⇔dy/dx= C/√y ⇔ √y ·dy=Cdx
Интегрируя последнее равенство, окончательно получаем
(2/3) ·y^(3/2) =Cx+C₁ -общее решение
Так как y(0)=1, то (2/3) ·1^(3/2) =C·0+C₁ ⇒ C₁=2/3
(2/3) ·y^(3/2) =1x+2/3 ⇒ частное решение y^(3/2) =1,5х+1
1.240 100%
х65%
х=240×65/100=15600/100=156кг
(нашли сколько продали)
2.теперь находим сколько осталось
240-156=84 кг
ОТВЕТ:осталось продать 84 кг.