Пошаговое объяснение:
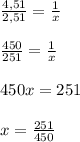
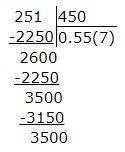
В решении.
Пошаговое объяснение:
Задача 1.
1) Найти, сколько дней потребуется второму трактористу, чтобы вспахать всё поле:
12 : 1 и 1/5 = 12 : 6/5 = (12*5)/6 = 10 (дней).
2) Найти, сколько дней потребуется третьему трактористу, чтобы вспахать всё поле:
10 * 1 и 1/2 = 10 * 1,5 = 15 (дней).
3) Чтобы найти, за сколько дней они вспашут поле, работая одновременно, нужно определить их производительность, какую часть поля они могут вспахать каждый за 1 день:
1 - всё поле.
1/12 - производительность 1 тракториста (1/12 поля в день).
1/10 - производительность 2 тракториста (1/10 поля в день).
1/15 - производительность 3 тракториста (1/15 поля в день).
Общая производительность:
1/12 + 1/10 + 1/15 = (5*1 + 6*1 + 4*1)/60 = 15/60 = 1/4 (поля в день).
Дней понадобится:
1 : 1/4 = 4 (дня).
4) Найти, какую часть поля за 4 дня вспашет каждый тракторист:
1/12 * 4 = 1/3 (часть поля) - 1 тракторист.
1/10 * 4 = 2/5 (части поля) - 2 тракторист.
1/15 * 4 = 4/15 (части поля) - 3 тракторист.
Проверка:
1/3 + 2/5 + 4/15 = (5*1 + 3*2 + 4)/15 = 15/15 = 1, верно.
Задача 2.
х - во второй цистерне нефти.
1 и 2/9*х - в первой цистерне нефти.
По условию задачи уравнение:
х + 1 и 2/9 х = 120
2 и 2/9 х = 120
х = 120 : 2 и 2/9
Перевести в неправильную дробь:
х = 120 : 20/9
х = (120 * 9)/20
х = 54 (т) - во второй цистерне нефти.
54 * 1 и 2/9 = 54 * 11/9 = (54*11)/9 = 66 (т) - в первой цистерне нефти.
Проверка:
54 + 66 = 120, верно.
Формула Кардано - методика определения корней кубического уравнения в поле комплексных чисел.
Впервые была опубликована в 1545 году итальянским математиком Джероламо Кардано.
Кубическое уравнение, выраженное в общем виде, как ах3+b х2+cx+d =0 в результате подстановки переменной:
приводится к виду неполного кубического уравнения, в котором не присутствует слагаемое, содержащее вторуюстепень: y3+b y +q=0,
где члены p и q приведены ниже:
Найдем Q:
Когда члены кубического уравнения вещественны, то и Q вещественное число, а по его знаку можно установить тип корней кубического уравнения.
Когда Q > 0 у кубического уравнения будет один вещественный корень и два сопряженных комплексных корня.
Когда Q = 0 у уравнения один однократный вещественный корень и один двукратный корень, или, в случае если p = q = 0, то получаем один трёхкратный вещественный корень.
Когда Q < 0 в кубическом уравнении будет три вещественных корня, но данный случай подробно не рассматривается.
По формуле Кардано, корни кубического уравнения в канонической форме будут равны:
где
Дискриминант многочлена у 3+ py + q в этом случае будет равняться:
.
Используя формулы Кардано, для всех найденных значений нужно выбрать такое , для которого осуществляется необходимое требование (такое значение всегда есть).
Когда искомое решение кубического уравнения вещественное число, то желательно отдавать преимуществовещественным значениям .
0.55 кг
Пошаговое объяснение:
4.5 - 1кг
2.51 - x
4.5.x = 2.51
x = 0.55