вот так
Поиск...
Избавься от ограничений
ПОПРОБУЙ ЗНАНИЯ ПЛЮС СЕГОДНЯ
alkaaskalka
19.07.2015
Математика
5 - 9 классы
ответ дан
От бревна отпилили сначала 30%, а потом 40% остатка. После этого длина оставшейся части бревна стала 2,1 м. Сколько метров отпилили от бревна во второй раз. Решите уравнением. ❤
1
СМОТРЕТЬ ОТВЕТ
Войди чтобы добавить комментарий
ответ
4,3/5
27
evvoronina1
профессор
4.8 тыс. ответов
7.9 млн пользователей, получивших
1) Пусть х - длина целого бревна.
Тогда 30х/100= 0,3х - отпилили сначала.
х - 0,3х - длина остатка после того, как отпилили 30%.
(х - 0,3х)•40/100 = 0,4(х - 0,3х) - отпилили потом.
Уравнение:
х - 0,3х - 0,4(х-0,3х) = 2,1
х - 0,3х - 0,4х + 0,12х = 2,1
1,12х - 0,7х = 2,1
0,42х = 2,1
х = 2,1 : 0,42
х = 5 м - длина целого бревна.
2) 0,4(х - 0,3х) = 0,4(5-0,3•5) = 0,4(5-1,5) =
= 0,4 • 3,5 = 1,4 м отпилили от бревна во второй раз.
ответ: 1,4 м.
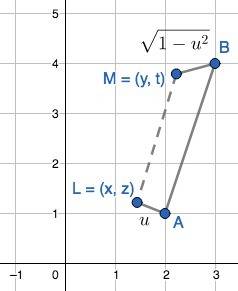
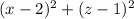– квадрат длины отрезка AL, 
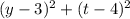– квадрат длины отрезка BM, 
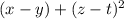– квадрат длины отрезка LM. 
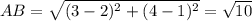. Поскольку по условию 
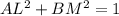, то AL, BM < 1, и минимальное значение LM (а значит, и 
) будет достигаться тогда, когда L и M лежат на отрезке AB.
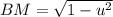, AL + BM = v. 
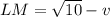будет минимально, когда v (и 
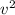) будет максимально.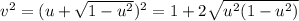
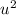, его максимум достигается в вершине, когда 
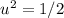, при этом 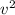достигает максимального значения 2, поэтому максимальное значение v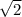 равно 
равно: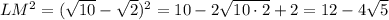
19
Пошаговое объяснение:
с начало умножение 32×3=96 потом 115-96=19