Используя формулу геометрической прогрессии найти p/q =0.2323233...

Question

Математика: Используя формулу геометрической прогрессии найти p/q =0.2323233...

nikolay946 · Accepted Answer

1. В 1 очередь надо найти область определения

Для левой части это будет x ≠ 2, ее же в этом случае приведем к виду

log√3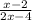 $\frac{x-2}{2x-4}$ =log√3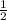 $\frac{1}{2}$

В правой части область определения x ≠ 2 и (x+1)/(x+2)>0, если x+1 >0 то и подавно x+2>0, если х+1 < 0 и x+2 <0, то x< -2, тогда x∈(-∞,-2)∪(-1,+∞), но с учетом x ≠2 имеем область определения x∈(-∞,-2)∪(-1,2)∪(2,+∞)

Теперь, избавляясь от логоарифмов

1/2= (x+1)/(x+2), x+2=2x+2

x =0

2. Тоже сначала ищем область определения

x²-9 ≥0, x ∈(-∞,-3]∪[3,+∞)

x+3 ≥ 0, x ∈ [-3,+∞)

x²+6x+9=(x+3)²≥0 ∀ x

Область определения в этом случае имеет вид x ∈ [3,+∞)

тогда имеем уравнение

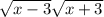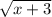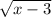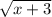
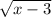$\sqrt{x-3} \sqrt{x+3}$ + $\sqrt{x+3}$ ≥x+3

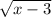$\sqrt{x-3}$ +1 ≥ $\sqrt{x+3}$

x-3+2 $\sqrt{x-3}$ +1≥x+3

2 $\sqrt{x-3}$ ≥5

x-3 ≥ 6,25

x ≥ 9,25

3. x=2y

x-y=y, x-y+1=y+1

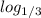$log_{1/3}$ 4y +

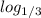$log_{1/3}$ 4y=0

4y=1,

y=0,25, x=0,5

Пошаговое объяснение:

MOGZ ответил