Пошаговое объяснение:
Решение задачи:
Пусть Х - это количество килограммов апельсинов в первом ящике, тогда
4 * Х - это количество килограммов апельсинов во втором ящике,
Х - 3 - это количество килограммов апельсинов в третьем ящике.
Составим уравнение:
Х + 4 * Х + Х - 3 = 75.
У выражение:
6Х - 3 = 75.
Перенесём цифру три из правой части уравнения в левую часть уравнения со знаком плюс:
6Х = 75 +3.
6Х = 78.
Найдём сколько килограммов апельсинов лежит в первом ящике:
Х = 78 / 6.
Х = 13 (килограммов).
Правильный ответ задачи: 13 килограммов апельсинов лежит в первом ящике.
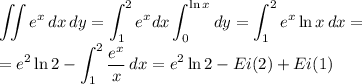
![\displaystyle\iint e^x\,dx\,dy=\int_0^{\ln 2}dy\int_{e^y}^2e^x\,dx=\int_0^{\ln2}(e^2-e^{e^y})\,dy=\\=e^2\ln2-\int_0^{\ln2}e^{e^y}\,dy=\left[\begin{array}{c}x=e^y\\y=\ln x\\dy=\frac{dx}{x}\end{array}\right]=\\=e^2\ln2-\int_1^2\frac{e^x}{x}\,dx=e^2\ln2-Ei(2)+Ei(1)](/tpl/images/0906/2547/de9e1.png)
в первой бригаде -на 7 больше чем во второй
во второй бригаде-?
всего 47