Пусть длина окружности переднего колеса х/м/, а заднего у/м/, тогда
120/х-120/у=6, если увеличить длину окружности переднего на 1/4 его длины, то она станет равной х+х/4=5х/4, а заднего у+у/5=6у/5,а значит
120/(5х/4)-120/(6у/5)=4, упростим первое уравнение. 120/х-120/у=6, получим 20/х-20/у=1; 20*(у-х)=ху; 20у-20х=ху;
упростим второе. (4*120/(5х))-(120*5/(6у))=4; 96у-100х=4;
24у-25х=ху;
20у-20х=24у-25х; 4у=5х, откуда х=4у/5;
24у-25*(4у/5)=у*4у/5; 4у-4у²/5=0; 4у(1-4у/5)=0; у=0; ∅; у=5, значит, длина окружности заднего колеса равна 5м, тогда переднего
5*(4/5)=4/м/
ответ 4м; 5м.

2,8
Пошаговое объяснение:Для решения нужно знать:
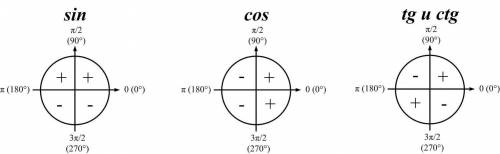
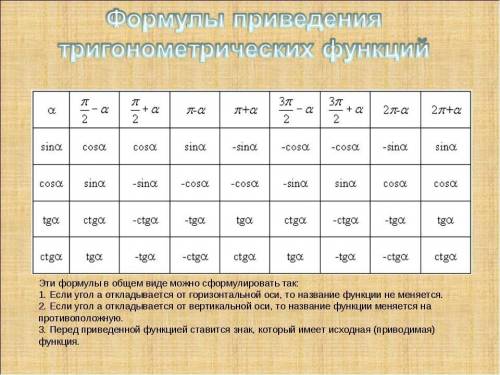
тригонометрическую окружность формулы приведенияосновное тригонометрическое тождество-10сos((7π/2)-α) = 10sinα, если начертить тригонометрическую окружность это можно доказать, но достаточно просто запомнить, что когда есть П/2, то функция меняется на противоположную.
sina=(1-cos^2(α))^(0,5)
sinα=(1-(-24/25)^2)^(0,5)= 0,28 теперь проверяем знак с тригонометрической окружности. 0,5пи до пи (п\2 до п) это соответствует II четверти, синус во второй четверти имеет знак +
10*0,28=2,8
3) (а + 17) + 23=40+а;
5) (18 + х) + 12=30+х;
6) (43 + y) + 57=100+у.
1) (9 + а) + 11=20+а;
2) (16 + b) + 4=20+b;
4) (b + 22) + 18=b+40;