
Пошаговое объяснение:
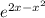 до члена с х^5:
до члена с х^5: =
= 
 = 1 + (-x) + (-x)^2/2! + (-x)^3/3! + (-x)^4/4! + O(x^5)
= 1 + (-x) + (-x)^2/2! + (-x)^3/3! + (-x)^4/4! + O(x^5)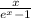 до члена с х^4:
до члена с х^4: = x \cdot \frac{1}{{e}^{x} - 1}
= x \cdot \frac{1}{{e}^{x} - 1} = x \cdot (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}) + x \cdot (1 - \frac{x}{1!} + \frac{x^2}{2!} - \frac{x^3}{3!} + \frac{x^4}{4!}) + O(x^5)
= x \cdot (1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!}) + x \cdot (1 - \frac{x}{1!} + \frac{x^2}{2!} - \frac{x^3}{3!} + \frac{x^4}{4!}) + O(x^5)
1.67+33+72+28=100
2.290+110+530=930
2.450:9+(670-590)*2
1.670-590=80
2.450:9=50
3.50+80=130
4.130*2=260