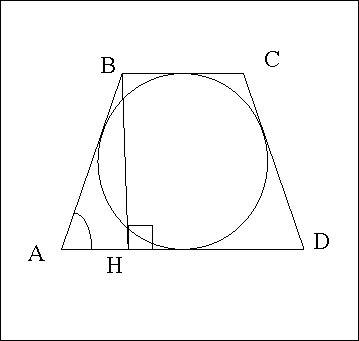
Дано:
АВСD -трапеция, описанная около окружности
АВ=СD - боковые стороны
ВС и АD - основания
<BAD = 30°
S ABCD = 98
Найти Р - периметр ABCD
Решение
1) S ABCD = (ВС+AD)*BH/2
Так как трапеция ABCD описана вокруг окружности, то у неё, как у любого четырёхугольника, описанного около окружности суммы противоположных сторон равны между собой.
ВС + AD = AB+CD.
А так как AB=CD, то ВС+AD=2AB.
Получаем периметр Р
Р = АВ+ВС+СD+AD = 4 AB
Р = 4·АВ
2) Тогда площадь S ABCD = 2АВ*BH/2 = АВ*ВН
S ABCD = АВ*ВН
3) Проведём ВН ┴ AD.
В прямоугольном ∆АВН по условию <BAD = 30°, значит, катет ВН, лежащий против угла в 30°, равен половине гипотенузы АВ.
ВН = АВ/2
4) Подставим ВН=АВ/2 в формулу площади S ABCD = АВ*ВН и получим:
АВ*АВ/2 = S ABCD
АВ² = 98*2
АВ² = 196
АВ = √196
АВ = 14
5) Наконец, находим периметр Р
Р = 4 AB
Р = 4 * 14 = 56
ответ: Р = 56
"Опасные" точки сразу видны, это:
1)
2)
Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
Выделяем целую часть в дроби:
Используем свойство 2-го замечательного предела, но добавляем степени:
То есть мы степень не меняли: домножили и разделили.
Посчитаем, что получилось:
Итак:
1)
2)
3)
4)
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).
Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.
Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала
Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).
Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).