Рассмотрим на двух примерах: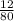 
и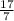 
1) Первым делом надо сократить дробь и сделать её правильной:
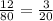
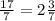
2) Затем есть два случая:
а) Знаменатель представляется в виде произведения степени двойки на степень пятёрки
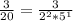
Домножаем числитель и знаменатель на нужную степень двойки/пятёрки, чтобы в знаменателе оказалась степень десятки
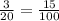
Переводим в десятичную дробь: записываем числитель, ставим запятую перед n-ной слева цифрой, где n - степень десятки в знаменателе (в нашем случае 2), при надобности дописываем необходимое количество нулей:
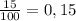
б) Знаменатель не представляется в виде произведения степени двойки на степень пятёрки (делится на простое число, не равное двум или пяти, в нашем случае - 7)
В таком случае, сделав дробь снова неправильной (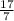) надо просто делить в столбик числитель на знаменатель, но предварительно поставив после числителя запятую и несколько нулей. Затем производит деление в столбик до тех пор, пока в вычитаемом (после приписывания нуля) не окажется то число, которое до этого уже было вычитаемым, когда уже приписывали нули после запятой:
_1 7,0 0 0 0 0 0 0 0 | 7
1 4 | 2,428571...
_3 0 <-- это число повторится
2 8
_2 0
1 4
_6 0
5 6
_4 0
3 5
_5 0
4 9
_1 0
7
3 0 <-- вот оно
С первого появления этого вычитаемого (включительно) до второго (не включительно) и будет период: В данном случае, когда первый раз появилось 30 (повторившееся вычитаемое), мы записали четвёрку (в данном случае она сразу после запятой, но так будет не всегда). Она - первая цифра в периоде. Когда во второй раз появилось 30 - мы (начиная с той четвёрки) записали 428571. Значит, это и есть период, т.е.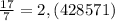 
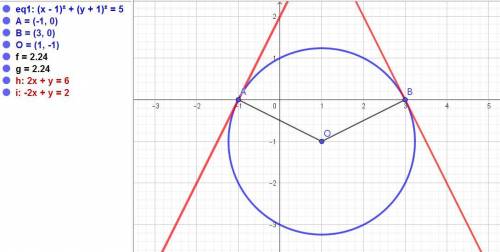
В точках пересечения окружности x²+y²-2x+2y-3=0 с осью Ох значение у = 0. Тогда x²-2x-3=0, Д = 4 - 4*(-3) = 16.
х₁ = (2 - 4)/2 = -1, х₂ = (2 + 4)/2 = 3.
Получили точки А(-1; 0) т В(3; 0).
Если выделить полные квадраты в уравнении, то получим:
(х - 1)² + (у + 1)² = 5.
Центр: точка О(1; -1).
Уравнение радиусов ОА и ОВ.
Векторы: ОА = ((-1 - 1); (0 - (-1)) = (-2; 1).
Векторы: ОВ = ((3 - 1); (0 - (-1)) = (2; 1).
Уравнение ОА: (х - 1)(-2) = (у + 1)/1, или у = (-1/2)х - (1/2).
Уравнение ОВ: (х - 1)(2) = (у + 1)/1, или у = (1/2)х - (3/2).
Уравнение касательной имеет угловой коэффициент к = -1/к(радиуса).
Уравнение касательной в точке А:
у = (-1/(-1/2))*х + в = 2х + в.
Для определения в подставим координаты точки А, через которую проходит касательная.
0 = 2*(-1) + в, отсюда в = 2.
Уравнение касательной в точке А: у = 2х + 2.
Аналогично находим в точке В: у = -2х + 6.
Можно находить уравнение касательной по формуле с производной, но в задании не оговорен этот
Пошаговое объяснение:
65-5=60 м ширина
Площадь участка равна 65*60=3900м²
3900*3/10 = 1170 м² площадь клумбы
так как 1 куст на каждые 2м² , то получим
1170:2= 585 кустов роз