А (кг)- нужно 1-му фермеру, в(кг) - нужно 2-му фермеру, с (кг) - нужно 3-му фермеру. Составляет систему уравнений: а+в+с=1957 (кг), Т.к. столько закупили всего три фермера.Второму надо в 5 раз меньше,чем первому: в=а/5. Третьему надо в 6 раз меньше,чем второму: с=в/6. Итак: а+в+с=1957, в=а/5, с=в/6.Выражаем из двух последних уравнений С и подставляет все в первое уравнение. С=в/6=> в=6*с. в=а/5=>а=5в=5*(6*с).Подставляем в первое уравнение: 5*6с+6с+с=1957, 37с=1957, с=52. 33/37. в=6*52.33/37.а=5*(6*52.33/37).Осталось посчитать эти дроби.
Возьмем самую распространенную дробь -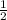
, или половину. 
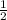=1:2
1 - числитель, 2 - знаменатель.
Чем больше числитель, тем больше дробь, чем больше знаменатель - тем больше дробь.
Сумму дробей можно найти, сложив числители в дробях с одинаковым знаменателем. Например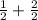
=
.
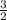То же самое с вычитанием.
А чтобы сложить/вычесть дроби с разными знаменателями, нужно свести их к общему знаменателю, найдя наименьшее общее кратное.
Например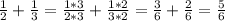
Чтобы умножить дроби, нужно умножить числитель на числитель, а знаменатель на знаменатель.
Чтобы поделить дроби, нужно умножить числитель на знаменатель, а знаменатель на числитель, то есть умножить на перевернутую дробь.