Пошаговое объяснение:
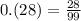
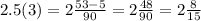
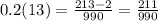
Рациональное число — это число, которое может быть представлено в виде дроби a разделить на b , где a — это числитель дроби, b — знаменатель дроби. Причем b не должно быть нулём, поскольку деление на ноль не допускается.
К рациональным числам относятся следующие категории чисел:
целые числа (например −2, −1, 0 1, 2 и т.д.)
обыкновенные дроби (например одна вторая, одна третья, три четвёртых и т.п.)
смешанные числа (например две целых одна вторая, одна целая две третьих, минус две целых одна третья и т.п.)
десятичные дроби (например 0,2 и т.п.)
бесконечные периодические дроби (например 0,(3) и т.п.)
Каждое число из этой категории может быть представлено в виде дроби a разделить на b .
Примеры:
Пример 1. Целое число 2 может быть представлено в виде дроби две первых . Значит число 2 относится не только к целым числам, но и к рациональным.
Пример 2. Смешанное число две целых одна вторая может быть представлено в виде дроби пять вторых. Данная дробь получается путём перевода смешанного числа в неправильную дробь
перевод двух целых одной второй в неправильную дробь
Значит смешанное число две целых одна вторая относится к рациональным числам.
Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби две десятых . Данная дробь получилась путём перевода десятичной дроби 0,2 в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему десятичных дробей.
Поскольку десятичная дробь 0,2 может быть представлена в виде дроби две десятых , значит она тоже относится к рациональным числам.
Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби три девятых. Данная дробь получается путём перевода чистой периодической дроби в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему периодические дроби.
Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби три девятых , значит она тоже относится к рациональным числам.
В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием — рациональные числа.
Надо превратить функции в уравнение и решить их, чтобы получить Х. После можно подставить значение Х и получить значение У. Чтобы проверить необходимо подставить значения в функцию, если равенства будут тождественно равны, то и точки пересечения правильные.
Пошаговое объяснение:
y=3-1/2x
y=x
3-1/2x=x
x+1/2x=3
3/2x=3
x=3:3/2
x=6/2*2/3
x=2
y=2
A(2;2)
y=1/2x+1
y=x-2
1/2x+1=x-2
x-1/2x=1+2
1/2x=3
x=3:1/2
x=6
y=6-2=4
A(6;4)
y=1/3x-2
y=-x
-1/3x-2=-x
-x+1/3x=-2
-2/3x=-2
2/3x=2
x=2:2/3
x=3
y=-3
A(3;-3)
у=-x-5
y=2x+4
-x-5=2x+4
2x+x=4+5
3x=9
x=9:3
x=3
y=-3-5=-8
A(3;-8)
y=x/3-2
y=5-2x
x/3-2=5-2x
x/3+2x=5+2
x/3+6x/3=7
7x/3=7
x=7:7/3
x=3
y=5-2*3=5-6=-1
Прямая зависимость (прямая пропорциональность)
A(0;0)
B(0;1)
Прямые параллельны
С(0;-3)
Прямые параллельны
Пошаговое объяснение:
Решение смотри на фото.