Если будешь использовать решение, предложенное Троллем, то вот формулы:
S - площадь треугольника со сторонами a, b, с
p - его полупериметр, т.е. (a+b+c)/2
r - радиус вписанной в него окружности
sqrt(z) - функция квадратного корня из величины z
S=(r/2)*(a+b+c)
S=sqrt(p*(p-a)*(p-b)*(p-c)) //ф-ла Герона
Подставив значения, получаем:
площадь треугольника (основания пирамиды) равна 336 см, радиус вписанной окружности равен 8 см
высота пирамиды из этого тоже равна 8 см. //по т. Пифагора
x - расстояния от основания высоты пирамиды до плоскостей боковых граней равны между собой, и выражаются в данном случае так:
x = sqrt(8^2-((8*sqrt(2))/2)^2) = sqrt(32) //по т. Пифагора
x = 4*sqrt(2) - "четыре корня из двух"
Пошаговое объяснение:
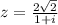
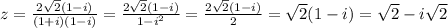
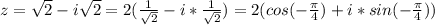
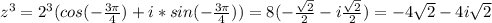
х+20 = 7
х 2
7х=2(х+20)
7х=2х+40
7х-2х=40
5х=40
х=40/5
х=8 - лет сыну
20+8=28 - лет матери
ответ: Маме 28 лет