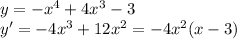
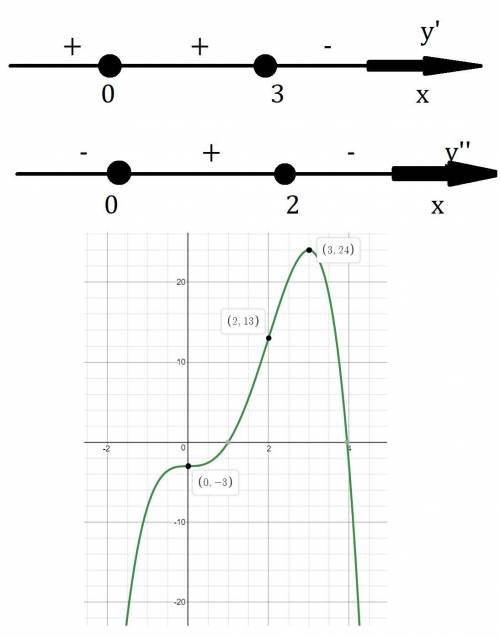
Как видно производная обращается в ноль при x=3 и x=0 это критические точки, используем метод интервалов, для определения знака производной на промежутках.
При x=0, производная не меняет знак, значит это не экстремум функции. При x=3, производная меняет знак с плюса на минус, значит это минимум функции.
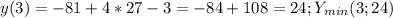
На (-∞;0)∪(0;3) функция растёт.
На (3;+∞) функция убывает.
Функция общего вида (не обладает чётность или нечётностью)
Найдём точки перегиба функции.
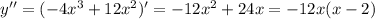
x=0 и x=2 это точки перегиба.
На (-∞;0)∪(2;+∞) функция выпукла вверх.
На (0;2) функция выпукла вниз.
Найдём координаты всего чего ещё не нашли.
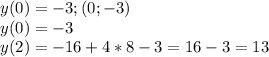
Можем строить.
Наименьшее значение (-∞;-∞) и (+∞;-∞)
Наибольшее значение (3;24)
 дана эта формуланужно исследовать её на монотонностьнайти н" />
дана эта формуланужно исследовать её на монотонностьнайти н" />
Привет. Я Владимир Путин. Я Царь России. Мне глубоко похрену на образование в Российской Федерации. Для России более важны состояние бордюра в Москве, состояние счета в моем швейцарском банке и личное счастье миллиардеров страны.
Я считаю, что имею полное право выдавать бюджетные деньги депутату Шапошникову, главе РосПриродНадзора и тому подобным высокопоставленным чиновникам. Голосуйте за меня и за мою партию, в которой я не состою ибо боюсь, и будет вам величайшая коррупция.
И главное. Поддержите поправки в конституцию РФ. Защитим кошек. Увековечим русский язык. Обнулим Путина.
Надеюсь, что счастливых дней у вас будет поменьше, а проблем - побольше Вам большое.
Объяснение:
Делителем натурального числа а называют натуральное число, на которое а делится без остатка. Число 12 имеет шесть делителей: 1, 2, 3, 4, 6 и 12. Число 1 является делителем любого натурального числа.
Признаки делимости
Признаки делимости на 2, 4, 8, 3, 9, 6, 5, 25, 10, 100, 1000, 11.
Признак делимости на 2. Число делится на 2, если его последняя цифра - ноль или делится на 2. Числа, делящиеся на два, называются чётными, не делящиеся на два – нечётными.
Признак делимости на 4. Число делится на 4, если две его последние цифры - нули или образуют число, которое делится на 4.
Признак делимости на 8. Число делится на 8, если три его последние цифры - нули или образуют число, которое делится на 8.
Признаки делимости на 3 и 9. Число делится на 3, если его сумма цифр делится на 3. Число делится на 9, если его сумма цифр делится на 9.
Признак делимости на 6. Число делится на 6, если оно делится на 2 и на 3.
Признак делимости на 5. Число делится на 5, если его последняя цифра - ноль или 5.
Признак делимости на 25. Число делится на 25, если две его последние цифры - нули или образуют число, которое делится на 25.
Признак делимости на 10. Число делится на 10, если его последняя цифра - ноль.
Признак делимости на 100. Число делится на 100, если две его последние цифры – нули.
Признак делимости на 1000. Число делится на 1000, если три его последние цифры – нули.
Признак делимости на 11. На 11 делятся только те числа, у которых сумма цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, делящееся на 11.
Существуют признаки делимости и для некоторых других чисел, однако они более сложные и в программе средней школы не рассматриваются.
П р и м е р . Число 378015 делится на 3, так как сумма его цифр равна:
3 + 7 + 8 + 0 + 1 + 5 = 24, а это число делится на 3. Данное
число делится на 5, так как его последняя цифра 5. Наконец,
это число делится на 11, так как суммы его чётных цифр:
3 + 8 + 1 = 12 и нечётных цифр 7 + 0 + 5 = 12 равны.
Но это число не делится на 2, 4, 6, 8, 9, 10, 25, 100 и 1000, так как …
А вот эти случаи вы проверите самостоятельно!