
ответ: лови 2, 3е не смогла)
Пошаговое объяснение:

ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
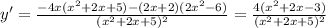
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
Пошаговое объяснение:
3х+2y+4x-y-2x+y 5x+2y
10c = 10c ОДЗ:с≠0
5а-1-7а+8-9а-7 -11а -11
14а = 14а=14 ОДЗ:а≠0
80с²-126с+56-40с+96с²-16с+16с²+32c
16с-8
192с²-182с+56
16с-8
с≠1/2