Пусть m- стоимость минуты разговора n -стоимость sms так как цены кратны копейке то m и n натуральные числа 13m+120n=2360 (коп) n=(2360-13m)/120 2360=2*2*2*5*59 120= 2*2*2*3*5 n=(2*2*2*5*59-13m)/2*2*2*3*5 чтобы полученное выражение было натуральным представим 13m в виде 13*p*2*2*2*3*5 где q -некоторое натуральное число n=(2*2*2*5*59-13p*2*2*2*3*5)/2*2*2*3*5=2*2*2*5(59-13p)/2*2*2*3*5= =(59-13p)/3 т.к. n натуральное то 59-13р>0 p<59/13≈4,5 то есть p может принимать значения от 1 до 4 из этих значений нам надо выбрать такие чтобы 59-13р ,было кратным 3 р=1, 59-13 не кратно3 р=2 59-26=33 кратно 3 р=3 59-39=20 не кратно 3 р=4 59-52=7 не кратно 3 таким образом р=2 n=(59-13*2)/3=(59-26)/3=33/3=11 (копеек)
Пошаговое объяснение:
По определению: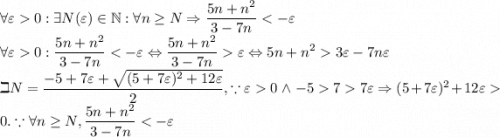
ЧТД
По определению:
ЧТД