все просто смотри
1)63:9=7(см)-дина 1 гвоздя
2)7-2=5(см)-станет длина гвоздя
3)30:5=6(г)
ответ:6 гвоздей
Пошаговое объяснение:1) f(x)= 2x²-3x+1 , [-1;1] ⇒ f'(x)= 4x-3, найдём критические точки: 4х-3=0, ⇒ х = 3/4=0,75 ∈[-1;1]. Найдём значения функции в критической точке и на концах данного промежутка: f(3/4)= 2·(3/4)²- 3·3/4 +1 =9/8 -9/4 + 1 = -1/8 ; f(1) = 0; f(-1)=6 ⇒ max f(x)=f(-1)=6; minf(x)=f(3/4)=-1/8
2)f(x)=3x²-4 на [2;4] ⇒ f'(x)=6x 6x=0, x=0-крит. точка, но x=0∉ [2;4] ⇒ Найдём значения функции на концах данного промежутка: f(2)= 3·2²-4= 12-4=8 f(4)=3·4² - 4= 48-4=44 ⇒ max f(x)=f(-4)=44; minf(x)=f(2)=8 3)f(x)=x²-1 на [0;3]⇒ f'(x)=2x , 2x=0 x=0 -критическая точка х=0 ∈ [0;3]. Найдём значения функции в критической точке и на концах данного промежутка: f(0) =0²-1=-1; f(3)=3²-1=8 ⇒max f(x)=f(3)=8; minf(x)=f(0)= -1
Пошаговое объяснение:
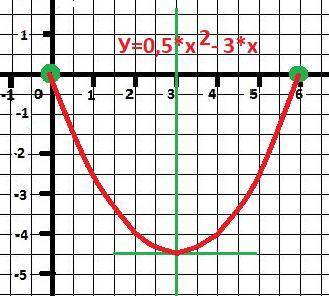
Дано: y =0,5*x²+-3*x+0 - квадратное уравнение.
Положительная парабола - ветви вверх.
Пошаговое объяснение: a*x² + b*x + c = 0 Вычисляем дискриминант - D.
D = b² - 4*a*c = -3² - 4*(0,5)*(0) = 9 - дискриминант. √D = 3.
Вычисляем корни уравнения.
x₁ = (-b+√D)/(2*a) = (3+3)/(2*0,5) = 6/1 = 6 - первый корень
x₂ = (-b-√D)/(2*a) = (3-3)/(2*0,5) = 0/1 = 0 - второй корень
6 и 0 - корни уравнения - точки пересечения с осью ОХ.
Минимальное значение по середине корней при Х=3
У(3) = 1/2*9 - 3*3 = 4.5 * 9 = - 4.5
Таблица с точками для построения графика - в приложении.
Рисунок с графиком в приложении.

1) 9-2=7
2) 30:7=4 гвоздя можно сделать.