Пошаговое объяснение:
№1
1-2/9=9/9-2/9=7/9 (осталось выполнить)
№2
70/105 (Сокращаем на 5)=14/21 (Сокращаем на 7)=1/3
№3
1/7+3/4 (домножаем для общего знаменателя 28)=4/28+21/28=25/28
№4
 =1114*(-35)/4=-38990/4 (сокращаем на 2)=-19495/2=-9747
=1114*(-35)/4=-38990/4 (сокращаем на 2)=-19495/2=-9747 =-9747,5
=-9747,5
№5
7/25*5=35/25 (сокращаем на 5)=7/5=1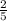 =1,4
=1,4
№6
9/28:18/35=(9*35)/(28*18) сокращаем 9 и 18 (делим на 9)=35/56=5/8
№7
5/6*х=4(1/2)
х=4(1/2)/(5/6)
х=27/5=5,4
№8
7/8*7/8=49/64
№9
5/7*35=25 (см)
№10
4(5/11)*22/98=49/11*22/98 (сокращаем (49 и 98) и (11 и 22))=2/2=1
№11
60/2*5=150
№12
Всего 68 га
Первый день 68*1/4=17 га
Второй день (68-17)*2/3=34 га
Третий день 68-17-34=17 га
№13
(7/12+11/30х):7/14=1/3
(7/12+11/30х)*14/7=1/3
22/30х=1/3-14/12
22/30х=-5/6
х=-25/22=-1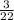
6) приравниваем выражение под модулем к нулю. x=3/4
Нарисуем интервал и разобьём его на 2 отрезка: (-беск. до 3/4] и (3/4 до +беск.)
Берём из первого интервала любое число, например -100. Подставляем в выражение 4x-3. Получается отрицательное число, значит знак на интервале (-беск. до 3/4] "-".
Аналогично, для второго интервала, берём число 100, подставляем. Знак интервала (3/4 до +беск.) "+".
Раскрываем модуль на 1-ом интервале:
-7/3(4x-3)+7,2=9
x= 39/70
Проверяем на интервале (-беск. до 3/4]
Данное число входит в этот интервал, значит является корнем.
Также на 2-ом, со знаком "+".
7/3(4x-3)+7,2=9
x=33/35
Проверяем на интервале (3/4 до +беск.). Данный корень является решением
ответ: x=39/70, x2=33/35
Задать вопрос
Войти
banner background
АнонимМатематика15 августа 01:53
Найдите значение выражение (4-14/33×1 1/21)×5 5/8
РЕКЛАМА
Выгодно с картой "Мир" на mos.ru
Перейти
ответ или решение2
Фадеев Макар
Выражение: (4 - 14/33 * 1 1/21) * 5 5/8 содержит скобки, действие умножения, дроби.
Определяем порядок действий
Сначала всегда выполняются вычисления в скобках. Смотрим: в скобках у нас вычитание и умножение. По правилу, первым делается умножение. В нашем примере: 14/33 * 1 1/21.
Умножаем простую дробь на смешанную
Для этого смешанную дробь 1 1/21 переводим в неправильную: 1 представляем как 21/21 и прибавляем 1/21. Получается: 22/21.
Перемножаем 14/33 и 22/21.
По правилам, надо просто умножить числитель на числитель (14 * 22), знаменатель на знаменатель (33 * 21).
Но не всегда надо идти по этому пути, ведь в нашем случае цифры довольно громоздкие.
Поэтому смотрим, есть ли возможность их сократить. Видим, что числа 14 (в числителе) и 21 (в знаменателе) можно сократить на 7, а числа 33 (в знаменателе) и 22 (в числителе) можно сократить на 11. В результате в числителе остается 2 * 2, в знаменателе 3 * 3. Результат: 4/9.
Вторым действием в скобках будет: 4 – 4/9.
Вычитаем дробь из целого числа
Для этого представим число 4 как 3 9/9. И тогда:
3 9/9 – 4/9 = 3 5/9.
Наконец, последнее действие — умножение на 5 5/8.
Перемножим смешанные дроби
Алгоритм этого действия такой: смешанные дроби превращаем в неправильные и перемножаем числители и знаменатели.
3 5/9 переводим в неправильную:
3 * 9 = 27;
27 + 5 = 32 (это и будет числитель).
Результат: 32/9.
5 5/8 переводим в неправильную:
5 * 8 = 40;
40 + 5 = 45 (это и будет числитель).
Результат: 45/8.
Теперь перемножаем 32/9 и 45/8.
Видно, что тут можно сократить 32 и 8 на 8, а 9 и 45 — на 9.
Остается: 4/1 * 5/1 = 20.
ответ: 20.