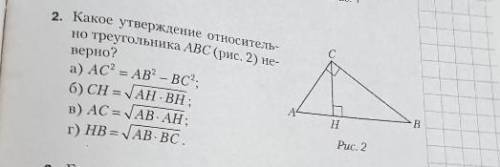
Відповідь:
Покрокове пояснення:
f(x)=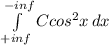 =1
=1
C∫_(-pi/2)^(pi/2) cos²xdx=C∫_(-pi/2)^(pi/2) (cos2x+1)/2 dx=
C/2 ∫_(-pi/2)^(pi/2) (cos2x+1)dx=C(1/4 sin2x+x/2) ║_(-pi/2)^(pi/2) =C(1/4*0+pi/4-0+pi/4)=C*pi/2=1 →C=2/pi
F(y)=2/pi \int\limits^{-inf}_{y} {cos^{2}x } \, dx=2/pi (1/4 sin2y+y/2)
M(x)=∫^{-inf}_{+inf}xf(x)dx=2/pi ∫_(-pi/2)^(pi/2) xcos²xdx=2/pi ∫_(-pi/2)^(pi/2) x(cos2x+1)/2 dx =1/pi ∫_(-pi/2)^(pi/2) (xcos2x+x) dx=
1/pi*(x²/2-x/2 sin2x+1/4 cos2x)║_(-pi/2)^(pi/2)=1/pi*0=0
D(x)=∫^{-inf}_{+inf} x²f(x)dx-(M(x))²=2/pi ∫_(-pi/2)^(pi/2) x²cos²xdx=
2/pi ∫_(-pi/2)^(pi/2) x²(cos2x+1)/2 dx=1/pi ∫_(-pi/2)^(pi/2) (x²cos2x+x²) dx=
1/pi*(x²/2*sin2x+x/2*cos2x-(sin2x)/4+x³/3)║_(-pi/2)^(pi/2)=1/pi*(pi/4*(-1)+pi/4*(-1)+pi³/12)=pi²/12-1/2=0,3225
стандартное отклонение
√D=√0,3225=0.56789
по 43 ученика, 13 аудиторий
Пошаговое объяснение:
Обозначим буквой a общий делитель чисел 172 и 387, тогда 172 = ax и 387 = ay. Получается, что в каждой аудитории разместили по a учеников, олимпиаду по химии писали в x = 172/a аудиториях, олимпиаду по литературе — в y = 387/a аудиториях.
Вычислим наибольший общий делитель 172 и 387 по алгоритму Эвклида:
387 = 172×2+43
172 = 43×4+0
Стало быть, НОД(172; 387) = 43. Впрочем, так как 43 — число простое, оно является единственным отличным от единицы общим делителем 172 и 387 (выделять отдельную аудиторию для каждого участника нерационально и так никто делать не будет).
Поэтому ответ получается однозначным, а именно: в каждой аудитории разместили по 43 ученика, а предоставили всего 172/43 + 387/43 = 4+9 = 13 аудиторий.