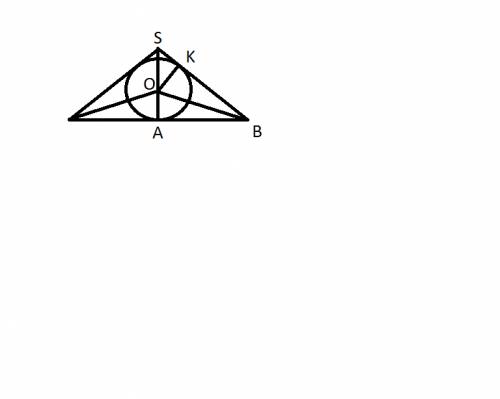
Рассмотрим треугольник одна вершина которого совпадает с вершиной пирамиды, а две другие - середины противолежащих сторон основания
SA = SB * sin ABS
SB = AB / cos ABS
AB = OB * cos ABO
OB = AO / sin ABO
учитывая, что AO = 1 по условию
AB = 2 (половина стороны основания)
2 = AB = OB * cos ABO = (AO / sin ABO) * cos ABO = cos ABO / sin ABO
или cos ABO = 2 sin ABO
угол ABS в два раза больше ABO. Поэтому по формулам преобразования двойных углов получим
SA = SB * sin ABS = (AB / cos ABS) * sin ABS =
= (2 / (cos^2 ABO - sin^2 ABO)) * 2 sin ABO cos ABO =
(подставим здесь формулу cos ABO = 2 sin ABO)
= 4 sin ABO (2 sin ABO) / (4 sin^2 ABO - sin^2 ABO) =
=8 sin^2 ABO / (3 sin^2 ABO) = 8/3
Объем пирамиды равен 1/3 hS = 1/3 * 8/3 * 4*4 = 128/9 = 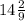
Пошаговое объяснение: удачи в учёбе!
ответ: смотрите ниже ↓↓
125/233 > 124/233
2/3⁽³ < 7/9 ( приведём к общему знаменателю)
6/9 < 7/9
9 цел.1/6 > 2 цел.4/7 ( тут общий знаменатель узнавать не обязательно, так как 9 больше 2.)
8 цел.3/8⁽³ < 8 цел.11/24
8 цел 9/24 < 8 цел 11/24
(( чтобы сравнить дроби надо: 1. привести их к общему знаменателю. 2. сравнить числители. ))