Видимо 4 объемных деталей конструктора если это расположить значение объема в порядке увеличения там множество учесть то можно прочесть слова обозначающие одно из важнейших ценностей

👇

Увидеть ответ

Ответ:

kseniya20072

23.01.2022

V:27

V:20

V:50

V:60

V:70 у меня была похожая задача во как я решала

Пошаговое объяснение:

4,4(28 оценок)

Открыть все ответы

Ответ:

seocer

23.01.2022

Написать уравнение касательной и нормали к графику функции y=sin(6x)-3 в точке х₀=π/18.

ответ:

а) y=(√3-6)/2+3x-π/6;

b) y=(√3-6)/2-1/3x+π/54.

Пошаговое объяснение:

Сначала вспомним общий вид уравнения касательной и нормали к графику функции y=sin(6x)-3 в точке х₀:

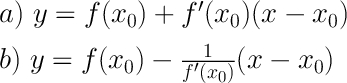
$\LARGE \boldsymbol {} a)\ y=f(x_0)+f'(x_0)(x-x_0)b)\ y=f(x_0)-\frac{1}{f'(x_0)} (x-x_0)$

где а - уравнение касательной, b - уравнение нормали.

Находим производную функции:

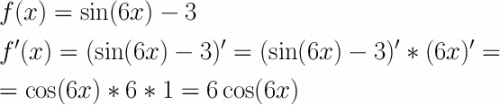
$\LARGE \boldsymbol {} f(x)=\sin(6x)-3f'(x)=(\sin(6x)-3)'=(\sin(6x)-3)'*(6x)'==\cos(6x)*6*1=6\cos(6x)$

Находим f'(x₀):

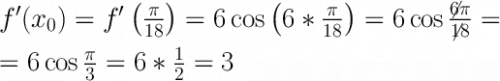
$\LARGE \boldsymbol {} f'(x_0)=f'\left(\frac{\pi }{18} \right) =6\cos\left(6*\frac{\pi }{18} \right)=6\cos\frac{\not6\pi }{\not18} ==6\cos\frac{\pi }{3} =6*\frac{1}{2}=3$

Находим f(x₀):

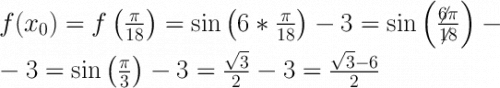
$\LARGE \boldsymbol {} f(x_0)=f\left(\frac{\pi }{18} \right) =\sin\left(6*\frac{\pi }{18} \right)-3=\sin\left(\frac{\not6\pi }{\not18} \right)--3=\sin\left(\frac{\pi }{3} \right)-3=\frac{\sqrt{3} }{2} -3=\frac{\sqrt{3} -6}{2}$

Мы имеем f(x₀), f'(x₀) и x₀. Подставляем в уравнение касательной:

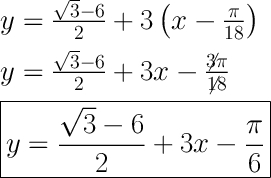
$\LARGE \boldsymbol {} y=\frac{\sqrt{3}-6 }{2}+3\left(x-\frac{\pi }{18}\right) y=\frac{\sqrt{3}-6 }{2}+3x-\frac{\not3\pi }{\not18} boxed{y=\frac{\sqrt{3}-6 }{2}+3x-\frac{\pi }{6}}$

Уравнение касательной имеет вид y=(√3-6)/2+3x-π/6.

Теперь подставляем f(x₀), f'(x₀) и x₀ в уравнение нормали:

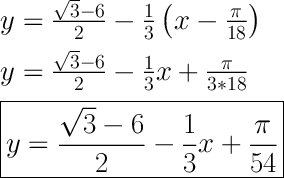
$\LARGE \boldsymbol {} y=\frac{\sqrt{3}-6 }{2} -\frac{1}{3}\left(x-\frac{\pi }{18}\right) y=\frac{\sqrt{3}-6 }{2} -\frac{1}{3}x+\frac{\pi }{3*18} boxed{y=\frac{\sqrt{3}-6 }{2} -\frac{1}{3}x+\frac{\pi }{54} }$

Уравнение нормали имеет вид y=(√3-6)/2-1/3x+π/54.

4,4(33 оценок)

Ответ:

2005SuperMax2005

23.01.2022

49. Запишем все двухзначные, что делятся на 7: 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98. Вычтем те, которые делятся на 21, то есть: 21, 42, 63, 84. Получим 14, 28, 35, 49, 56, 70, 77, 91, 98. Вместе 9 чисел.

50. Запишем все двухзначные, что делятся на 8: 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96. Вычтем те, которые делятся на 16, то есть: 16, 32, 48, 64, 80, 96. Получим 24, 40, 56, 72, 88. Вместе 5 чисел.

51. Запишем все двухзначные, что делятся на 8: 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96. Вычтем те, которые делятся на 24, то есть: 24, 48, 72, 96. Получим 16, 32, 40, 56, 64, 80, 88. Вместе 7 чисел.

52. Запишем все двухзначные, что делятся на 9: 18, 27, 36, 45, 54, 63, 72, 81, 90, 99 Вычтем те, которые делятся на 36, то есть: 36, 72. Получим 18, 27, 45, 54, 63, 81, 90, 99. Вместе 8 чисел.

4,6(86 оценок)

Это интересно:

Взаимоотношения

29.12.2020

Как игнорировать своего парня: 5 советов для девушек, которые хотят сохранить свою независимость...

Стиль-и-уход-за-собой

26.11.2020

Как сделать боб каре как у Пэрис Хилтон...

Кулинария-и-гостеприимство

31.05.2023

Как приготовить банановый смузи без блендера: простые и эффективные методы...

Дом-и-сад