1.Найдите производную функции в точке x=1: y=-7x^3+5√x. 2.Вычислите интеграл: ∫▒〖(x^3-2x+5)dx.〗
3.Найдите решение дифференциального уравнения:
y^'-y=0;
3y"+4y'+y=0.

👇

Ответ:

Uliana1pa

16.07.2021

Выражение в€«в–’гЂ–(x^3-2x+5)dx.гЂ— для дальнейших вычислений представлено в математическом виде как x*x-x-(x^3-2*x+5)*dxx. Переменная dxx не является ни числом, ни функцией. Допустимые переменные: x. Допустимые функции: exp, log, sqrt, atanh, asech, acsch, acoth, atan, acosh, asinh, acos, asin, acot, cosh, sinh, tanh, sech, csch, coth, sin, cos, tan, cot, ln, sec, factorial. Допустимые выражения: 3*x, 2*pi, infinity, e ≡ exp(1) а остальное незнаю

4,5(9 оценок)

Ответ:

Влад11737463

16.07.2021

Пошаговое объяснение:

4,7(40 оценок)

Открыть все ответы

Ответ:

LoveSmile78900987

16.07.2021

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
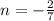1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

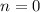- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

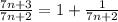
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

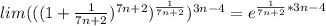$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

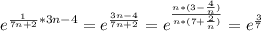$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

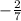
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

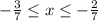Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност

4,4(95 оценок)

Ответ:

andrievskiyvitaliy

16.07.2021

По значению тангенса можно найти значение косинуса. Их связывает одно очень важное соотношение:

1 + tg²t = 1 / cos²t

Отсюда выразим квадрат косинуса:

cos²t = 1 / (1 + tg²t)

Теперь подставим значения в данное выражение и найдём квадрат косинуса:

cos²t = 1 / (1 + 49/576) = 1 : 625/576 = 576/625

Следовательно, по квадратному уравнению получаем два возможных значения косинуса:

сos t = 24/25 или cos t = -24/25

Какой косинус выбрать - положительный или отрицательный? По условию значение угла лежит в промежутке от π до 3π/2. Поэтому, угол лежит в 3 четверти, где косинус как мы знаем отрицательный. Поэтому, cos t = -24/25.

Теперь элементарно вычислить например котангенс угла. Получаем по соотношению между тангенсом и котангенсом:

ctg α = 1 / tg α = 1 : 7/24 = 24/7

Синус угла легко найти, зная косинус и например тангенс(всё это мы знаем).

tg α = sin α / cos α

Отсюда

sin α = tg α * cos α = 7/24 * (-24/25) = -7/25

Задача решена.

4,5(25 оценок)

Это интересно:

Компьютеры-и-электроника

09.03.2021

Изучаем, как создать общедоступный календарь в Outlook...