Масса третьего сплава x кг, серебра в нём 0,23x кг.
Масса первого сплава (x-8)/2 кг, серебра в нём 0,2·(x-8)/2 = 0,1·(x-8).
Масса второго сплава (x-8)/2+8 кг, серебра в нём 0,25·((x-8)/2+8) = 0,125·(x-8)-2 кг.
Масса серебра в первых двух сплавах равна массе серебра в третьем сплаве:
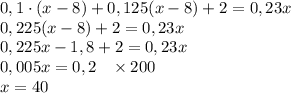
Можно решить по-другому:
Пусть x кг - масса первого сплава, серебра в нём 0,2x кг. Масса второго сплава (x+8) кг, серебра в нём 0,25·(x+8) кг.
Масса третьего сплава x+x+8 = (2x+8) кг, серебра в нём (0,2x+0,25·(x+8)) кг, что составляется 23%. То есть отношение массы серебра к массе сплава равно 0,23
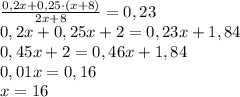
Масса первого сплава 16 кг, масса второго 16+8 = 24 кг, масса третьего 16+24 = 40 кг.
Такого прямоугольника нет, например, если умножить 110*111=12210 см кв., если умножить 111*112=12432 см. кв. Число 12345 попадает в этот промежуток площадей, данное значение невозможно получить из натуральных чисел с разницей в единицу..
Доказать это можно так, приняв одну из сторон за Х:
Х(Х+1)=12345
Решаем квадратное уравнение Х^2+Х-12345=0, находим дискриминант
Д=49381 (Корень из данного значения выделить в натуральном выражении невозможно. С округлением - это 222,218. Следовательно, и корни квадр. уравнения не будут натуральными числами.).Можно вычислить корни только с приближением (округлением):
Х1=(-1+222,218)/2= 110,61 или Х2=(-1-222,218)/2=-111,61
Пошаговое объяснение:
1)
х + 7/12 = 3/4
х = 9/12 - 7/12
х = 2/12
х = 1/6
2)
х - 1/6 = 1/9
х = 1/9 + 1/6
х = 2/18 + 3/18
х = 5/18
3)
х - 3/5 = 3/8
х = 3/8 + 3/5
х = 15/40 + 24/40
х = 39/40
4)
х + 5/24 = 7/12
х = 14/24 - 5/24
х = 9/24
х = 3/8
5)
у + 2/7 = 1/3
у = 1/3 - 2/7
у = 7/21 - 6/21
у = 1/21
6)
х - 1/6 = 7/9
х = 14/18 + 3/18
х = 17/18
7)
у - 3/8 = 5/32
у = 5/32 + 12/32
у = 17/32
8)
у + 2/5 = 1/2
у = 5/10 - 4/10
у = 1/10