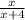- данная дробь, знаменатель на 4 больше числителя.
Если числитель увеличить на 6, а знаменатель на 4, то получим
,
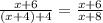то дробь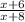 
возрастает менее чем вдвое по сравнению с дробью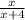
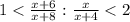
Если же числитель увеличить на 8, а знаменатель на 1,
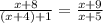
то дробь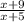 
увеличивается более чем втрое по сравнению дробью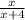
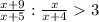
Решаем систему: x≠-4
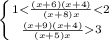
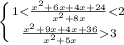
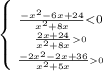
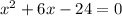
D=132
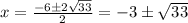
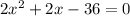
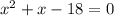
D=1+72
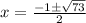
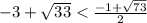
При x=3 получим дробь 
которая удовлетворяет указанным условиям
При x=3 получим дробь
которая удовлетворяет указанным условиям
Если числитель увеличить на 6, а знаменатель на 4, то получим
, 
, 
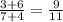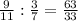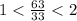
Если же числитель увеличить на 8, а знаменатель на 1,
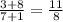
то дробь увеличивается более чем втрое по сравнению дробью
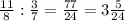
3/7
Пошаговое объяснение:
x - числитель.
Начальная дробь: x/(x+4), где x - натуральное число.
Система неравенств:
(x+6)/(x+4+4)<(2x)/(x+4); (x+6)/(x+8)<(2x)/(x+4)
(x+8)/(x+4+1)>(3x)/(x+4); (x+8)/(x+5)>(3x)/(x+4)
(x+6)(x+4)<2x(x+8)
x²+4x+6x+24<2x²+16x
2x²+16x-x²-10x-24>0
x²+6x-24>0
Допустим: x²+6x-24=0; D=36+96=132
x₁=(-6-2√33)/2=-3-√33 - этот корень не подходит для уравнения, так как x - натуральное число.
x₂=(-6+2√33)/2=√33 -3 - этот корень также не подходит для уравнения, так как x - натуральное число.
При 0≤x<√33 -3: (2+6)/(2+8)<(2·2)/(2+4); 24/30>20/30 - неравенство не выполняется.
При x>√33 -3: (3+6)/(3+8)<(2·3)/(3+4); 21/28<24/28 - неравенство выполняется.
Следовательно, для данного 1-го неравенства x∈[3; +∞).
(x+8)(x+4)>(3x)(x+5)
x²+4x+8x+32>3x²+15x
3x²+15x-x²-12x-32<0
2x²+3x-32<0
Допустим: 2x²+3x-32=0; D=9+256=265
x₁=(-3-√265)/4 - этот корень не подходит для уравнения, так как x - натуральное число.
x₂=(√265 -3)/4 - этот корень также не подходит для уравнения, так как x - натуральное число.
При x>(√256 -3)/4: (4+8)/(4+5)>(3·4)/(4+4); 8/6<9/6 - неравенство не выполняется.
Отсюда следует, что x=3 - это числитель.
Знаменатель: 3+4=7.
Дробь: 3/7.