65+44 = 109
387+646= 1033
538+758= 1296
244+648= 892
3 гири весами 3 (единиц), 4 (единиц) и 5 (единиц)
Пошаговое объяснение:
Рассмотрим варианты по числу гирь, начиная с наименьшего числа гирь.
Число гирь не может быть равным 2, так как в первом случае тяжёлая из гирь 2 раза тяжелее чем лёгкая, а во втором случае тяжёлая из гирь 3 раза тяжелее чем лёгкая.
Рассмотрим гири весами: 3 (единиц), 4 (единиц) и 5 (единиц). Тогда:
1) в первом случае:
в левой руке гиря весом 4 (единиц), а в правой руке гири весами 3 (единиц)+5 (единиц) = 8 (единиц), то есть в 2 раза тяжелее другой;
2) во втором случае:
в левой руке гиря весом 3 (единиц), а в правой руке гири весами 4 (единиц)+5 (единиц) = 9 (единиц), то есть в 3 раза тяжелее другой.
Знак неравенства меньше нуля, значит, нужно, чтоб квадратичная функция была расположена ниже оси абсцисс. Для этого требуется установить направление ветвь параболы. Очевидно, же что, когда ветви параболы направлены вниз и D<0(дискриминант меньше нуля), неравенство выполняется для всех действительных значения х.
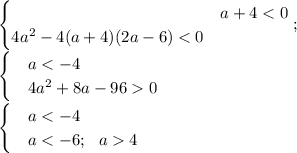
Получаем решение системы неравенств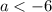 
. То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.
1-109
2) 1033
3) 1296
4) 892
Пошаговое объяснение: