Question

ABCD - любой четырёхугольник I, J, K и L середины сторон AB, BC, CD, DA
Докажите, что вектор IJ = 1/2 вектор АС

Answer 1

(в приложении рисунок)

Вот смотри. Мы начертили произвольный четырехугольник ABCD и отметили все точки, какие было нужно, а теперь будем рассматривать треугольник ABC и треугольник IBJ. Нам нужно доказать, что IJ=1/2AC, иначе говоря, оказать, что AC=2IJ. Что мы имеем? AI=IB, так как I - это середина AB; BJ=JC, так как J - это середина BC. Тогда AB=2BI, а BC=2BJ. Так же ΔABC и ΔIBJ имеют общий угол B, то есть ∠АВС=∠IBJ. И теперь мы видим что ΔABC и ΔIBJ подобны по второму признаку подобия треугольников, по двум сторонам и углу между ними ($\frac{AB}{BI} =\frac{BC}{BJ}$   и ∠АВС=∠IBJ). Подобные треугольники - это треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. В таком случае, все стороны пропорциональны $\frac{AB}{BI} =\frac{BC}{BJ}=\frac{AC}{IJ}$ . 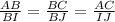Теперь найдем их пропорциональное соотношение:

$\frac{AC}{IJ}=\frac{AB}{BI};\\\frac{AC}{IJ}=\frac{2BI}{BI};\\\frac{AC}{IJ}=2$

или  $\frac{IJ}{AC}=\frac{1}{2}$ .

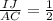P.S. Вот и всё, надеюсь, понятно.