
Если для любого  из области определения функции выполняется равенство
из области определения функции выполняется равенство 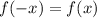 , то функция является чётной.
, то функция является чётной.
Если для любого  из области определения функции выполняется равенство
из области определения функции выполняется равенство 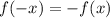 , то данная функция является нечётной.
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
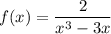
Отсюда 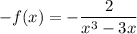 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:

Итак, область определения нашли. Теперь найдём 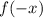 , для этого все
, для этого все  в функции заменим на
в функции заменим на 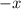 .
.
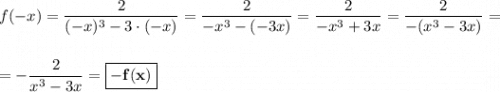
Таким образом, данная функция является нечётной.
в)
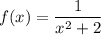
Отсюда 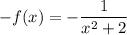 .
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
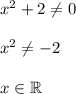
То есть, для данной функции за  можно принять любое действительное число. Теперь найдём
можно принять любое действительное число. Теперь найдём 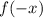 , для этого все
, для этого все  в функции заменим на
в функции заменим на 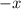 .
.
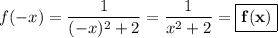
Таким образом, данная функция является чётной.
г)
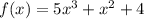
Отсюда 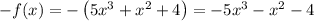 .
.
 может быть любым числом, поскольку никаких ограничений на аргумент здесь не накладывается. Теперь найдём
может быть любым числом, поскольку никаких ограничений на аргумент здесь не накладывается. Теперь найдём 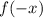 , для этого все
, для этого все  в функции заменим на
в функции заменим на 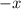 .
.
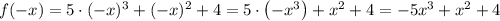 .
.
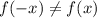 и
и 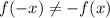 , а значит, функция не является ни чётной, ни нечётной.
, а значит, функция не является ни чётной, ни нечётной.
запись числа :
34
52
76
93
17
70
Десятки "
34-3 десятка
52-5
76-7
93-9
17-1
70-7
Единицы :
34-4 единица
52-2
76-6
93-3
17-7
70-0