Предположим противное, то есть то, что Вася всегда сможет выписать очередное число. В силу попарного различия выписываемых чисел, их множество неограниченно.
Рассмотрим первые 9 чисел. Пусть у них есть общий делитель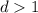 
. Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель 
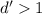. Если при этом 
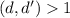, то можно взять первые 10 чисел и у них окажется общий делитель 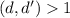, противоречие. Значит, 
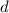и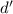 
взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.
Пошаговое объяснение:
1) x^2 + y^2 + 4y - 20 = 0
x^2 + (y^2 + 4y + 4) - 4 - 20 = 0
x^2 + (y + 2)^2 = 24 = (2√6)^2
Да, это уравнение окружности с центром A(0; -2) и R = 2√6
2) Гипербола, 2b = 8; e = 3√5/5
b = 4; b^2 = 16
e = √(a^2 + b^2)/a = 3√5/5
√(a^2 + 16)/a = 3√5/5
3a*√5 = 5√(a^2 + 16)
9a^2*5 = 25(a^2 + 16)
45a^2 = 25a^2 + 400
20a^2 = 400
a^2 = 400/20 = 20; a = √20 = 2√5
Каноническое уравнение гиперболы:
x^2/20 - y^2/16 = 1
3. Парабола x^2 = -32y
Каноническое уравнение параболы:
x^2 = 2p*y
p = -32/2 = -16
Фокус: F(p/2; 0) = (-8; 0)
Директриса: x = -p/2 = 8