Пошаговое объяснение:
20 мин= 1/3 часа
8/9:1/3=8/9*3=8/3 = 2 2/3 км/ч скорость пешехода
Пошаговое объяснение:
расстояние 40 км
начальная скорость х км/час
планируемое время --- 40/х час
половина расстояния --- 40 : 2 = 20 (км)
время с нач. скоростью 20/х час
увеличенная скорость --- (х+20) км/час
путь с увеличенной скоростью 20 + 40 = 60 (км)
время с увеличенной скоростью 60/(х+20) (час)
все время движения --- [20/х + 60/(х+20)] (час)
превышение запланированного времени 20/х + 60/(х+20) - 40/х = 60/(х+20) - 20/х
разница времени по условию 21/60 = 7/20 часа
уравнение для решения задачи 60/(х+20) - 20/х = 7/20
60/(х+20) - 20/х = 7/20 |*20х(х+20)
1200х - 400х - 8000 = 7х² + 140х
7х² - 660х + 8000 = 0
D = 660² - 4*7*8000 = 435600-224000 = 211600 = 460²
х₁ = (660 + √(460²) )/14 = (660 + 460)/14 = 1120/14 = 80 (км/час)
х₂ = (660 - 460)/14 = 100/7 = 14 целых 2/7 (км/час)
ответ: 80 км/час; 14 целых 2/7 км/час
Если будешь использовать решение, предложенное Троллем, то вот формулы:
S - площадь треугольника со сторонами a, b, с
p - его полупериметр, т.е. (a+b+c)/2
r - радиус вписанной в него окружности
sqrt(z) - функция квадратного корня из величины z
S=(r/2)*(a+b+c)
S=sqrt(p*(p-a)*(p-b)*(p-c)) //ф-ла Герона
Подставив значения, получаем:
площадь треугольника (основания пирамиды) равна 336 см, радиус вписанной окружности равен 8 см
высота пирамиды из этого тоже равна 8 см. //по т. Пифагора
x - расстояния от основания высоты пирамиды до плоскостей боковых граней равны между собой, и выражаются в данном случае так:
x = sqrt(8^2-((8*sqrt(2))/2)^2) = sqrt(32) //по т. Пифагора
x = 4*sqrt(2) - "четыре корня из двух"
Пошаговое объяснение:
1)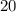 мин =
мин = 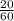 часа =
часа = 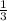 часа
часа
2)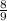 км :
км : 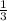 ч =
ч = 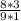 км/ч =
км/ч = 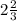 км/ч
км/ч
ответ: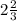 км/ч
км/ч