
Дано уравнение 9x² - 25y² - 225 = 0.
Перенесём свободный член направо и разделим на него обе части.
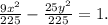
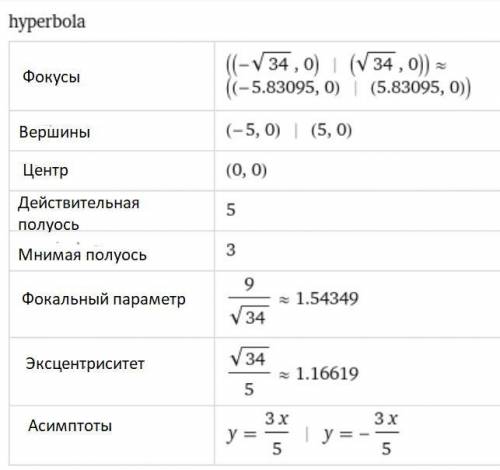
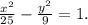 Получили уравнение гиперболы.
Получили уравнение гиперболы.
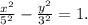 Из него сразу виды величины полуосей:
Из него сразу виды величины полуосей:
действительная а = 5 и мнимая b = 3.
c — расстояние от центра C до любого из фокусов, F1 и F2, находим
с = √(a² + b²) = √(5² + 3²) = √(25 + 9) = √34.
Эксцентриситет e = c/a = √34/5.
Уравнения асимптот находятся из уравнения гиперболы, но 1 заменить на 0.
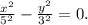
Разложим левую часть как разность квадратов.

Отсюда получаем уравнения двух асимптот.
y = 3x/5 y = -3x/5.

2)tg^2 a* cos^2 a+ctg^2 a*sin^2 a = ((sin²a*cos²a) / cos²a) + +((cos²a*sin²a ) / sin²a) = sin²a + cos²a = 1.
3)cos^4 a+sin^2 a*cos^2 a+sin^2 a = cos²a*(cos²a + sin²a) + sin²a = =cos²a*1 + sin²a = 1.
4) tg a/(1-tg^2 a) +ctg a /(1-ctg^2 a) =
= 2*sin a *cos² a / 2*cos a*cos (2a) +
+ 2*cos a*sin²a / 2*sin a*(-cos (2a)) = tg (2a) / 2 - tg (2a) / 2 = 0.
5)sin^2 a+cos^2 a+ tg^2 a = = 1 + sin² a / cos²a = (cos²a + sin²a) / cos²a = 1 / cos²a.
6) sin a /(1+cos a) + sin a /(1-cos a) =
= (sin a - sin a*cos a + sin a + sin a*cos a) / (1 – cos2a) = 2*sin a / (1 – -cos²a) = 2*sin a / sin²a = 2 / sin a.