ДАНО
Y= x/(x²-4)
ИССЛЕДОВАНИЕ
1.Область определения D(x). В знаменателе не ноль. (x²-4)=(x-2)(x+2)≠0
Х∈(-∞;-2)∪(-2;2)∪(2;+∞).
Вертикальных асимптоты (две) - х1 = -2,.х2 = 2.
2. Пересечение с осью Х. Y=0 при х = 0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.(Делим и числитель и знаменатель на Х в степени числителя)
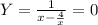
limY(+∞) = 0.
Горизонтальная асимптота Y=0.
5. Исследование на чётность.Y(-x) = - Y(x).
Функция нечётная.
6. Производная функции.
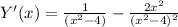
Корней - нет.
7. Локальные экстремумы.Максимума и минимума – нет.
8. Интервалы монотонности.
Убывает на всем интервале определения.
9. Вторая производная - Y"(x).
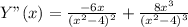
Корни производной - точки перегиба: х = 0 и в точках разрыва вычисляем пределы при х = +/-2.
9. Выпуклая “горка» Х∈(-∞;-2)∪(0;2), Вогнутая – «ложка» Х∈(-2;0)∪(2;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(∞)(k*x+b – f(x).
k=lim(∞)Y(x)/x = 1/(x²-4) = 0. Совпадает с горизонтальной асимптотой.
12.График в приложении.
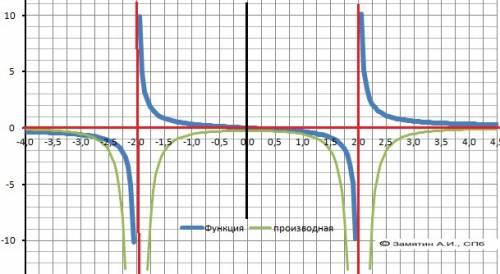
Расчет проведен в таблице - в приложении.
РЕШЕНИЕ с пояснениями - лишние слова можно и удалить.
Событие - выбрать СЛУЧАЙНУЮ БРАКОВАННУЮ состоит из двух.
Вероятность деталей в партии - р1(i) - найдем по количеству работников.
p11 = 2/10 = 0,2, аналогично - p21=0,5, p31=0,3.
Вероятность брака - q2(i) - дано. Для общности найдем вероятность годной детали у каждого работника.
p21=1-q11 = 0,98, p22=0,97, p23 = 0,95.
ГЛАВНОЕ: Вероятность нашего события - "выбрать И случайную И бракованную ИЛИ 5р ИЛИ 4р ИЛИ 3р равна СУММЕ ПРОИЗВЕДЕНИЙ вероятности каждого из возможных.
Заполняем столбики - любая годная и любая бракованная и находим сумму произведений.
Sq = 0,2*0,02 + 0,5*0,03 + 0,3*0,05 = 0,004+0,015+0,15=0,034= 3,4% - случайная бракованная - ОТВЕТ
Не трудно найти и вероятность случайной годной - Sp =0,966=96,6%.
Проверяем - сумма вероятностей равна 1.
ДОПОЛНИТЕЛЬНО
По формуле Байеса можно посчитать, что эту бракованную деталь с равной вероятностью 44,1% могли сделать и 4 и 3р.
А вот годную - с вероятностью 50,2% - четвертый разряд.