
а)
2x +3 y = 10
-2x + 5y = 6
2x+3y = 10
-2x = 6 - 5y
2x+3y = 10
2x = -6 + 5y
Подставляем -6 + 5у вместо 2х в первое уравнение
-6 + 5y + 3y = 10
8y = 10 + 6
8y = 16
y = 16/8
y = 2
Теперь y = 2 подставим в уравнение 2x = -6 + 5y
2x = -6 + 5*2
2x = -6 + 10
2x = 10 - 6
2x = 4
x = 4/2
x = 2
Проверяем (Подставляем x и y в исходные уравнения)
2*2 +3*2 = 10
4 + 6 = 10
Верно
-2*2 + 5*2 = 6
-4 + 10 = 6
10 - 4 = 6
Верно.
б)
3x - y =2
x + 2y = 10
3x - y =2
x = 10 - 2y
Подставялем в первое уравнение 10 - 2y вместо x
3*(10-2y) - y = 2
30 - 6y - y = 2
-7y = -28
7y = 28
y = 28/7
y = 4
Подставляем y = 4 в уравнение x = 10 - 2y
x = 10 - 2*4
x = 10 - 8
x = 2
Проверяем, подставив y = 4 и x = 2 в исходные уравнения
3*2 - 4 = 2
6 - 4 = 2
Верно
2 + 2*4 = 10
2 + 8 = 10
Верно.
1a)
1б)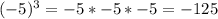
1в)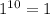
1г)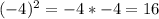
1д)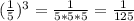
2a)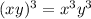
2б)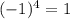
2в)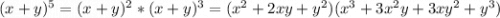
3a)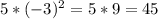
3б)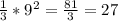
3в)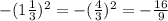
3г)