(8 5/7-6 5/6:1 5/36)•4/9
(61\7-41\6*5\36)*4\9
(61\7-205\216)*4\9
11741\1512*4\9
11741/378*1/9
11741/3402
3 1535\3402
* - це помножити
Пошаговое объяснение:
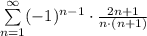
Исследуем этот ряд на абсолютную сходимость.
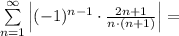
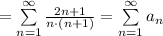
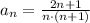
Рассмотрим ряд
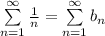
Используем предельный признак сравнения:
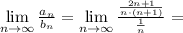
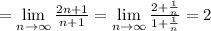
Значит ряды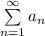 
и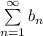 
сходятся или расходятся одновременно, но ряд
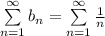
это гармонический ряд, который расходится. Значит и ряд
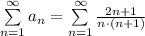
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
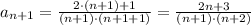
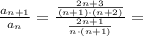
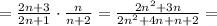
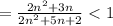
т.к.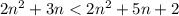 
⇔ 
⇔ 
.
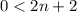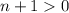То есть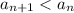 
.
То есть последовательность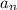 
монотонно убвывает.
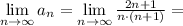
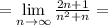
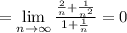
То есть последовательность 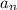монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
Відповідь:
1) 6 5\6:1 5\36=5,7
2) 8 5\7 - 5,7 = 3
3)3* 4\9= 1,3
Покрокове пояснення: