х₁=-4; х₂=-0,8
Пошаговое объяснение:
Раскрываем модуль и решаем как обычные уравнения. Вместе с этим обязательно нужно принимать во внимание, что при раскрытии модуля число модуля может быть как положительным так и отрицательным. После раскрытия модуля получаем уравнение:
0,5х-2=2х+4
2х-0,5х=-2-4
1,5х=-6
х=-6:1,5
х₁=-4
Проверка: (подставляем в уравнение найденное значение х₁=-4)
0,5*(-4)-2=2*(-4)+4
-2-2=-8+4
-4=-4
Дальше рассмотрим второй случай, с модулем отрицательного числа
0,5х-2=-2х-4
0,5х+2х=-4+2
2,5х=-2
х=-2:2,5
х₂=-0,8
Проверка: (подставляем в уравнение найденное значение х₂=-0,8
0,5*(-0,8)-2=-2*(-0,8)-4
-0,4-2=1,6-4
-2,4=-2,4
Решение: Запишем ОДЗ: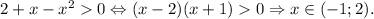
Переходим к уравнению-следствию: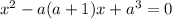
.
Найдём дискриминант:![D=[-a(a+1)]^2-4\cdot1\cdot a^3=a^4+2a^3+a^2-4a^3=a^4-2a^3+a^2=a^2(a^2-2a+1)=a^2(a-1)^2=[a(a-1)]^2.](/tpl/images/2005/6762/e07c3.png)
Дискриминант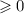
при любых значениях параметра, а значит квадратное уравнение всегда имеет корень. При 
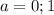дискриминант равен 0 и уравнение имеет единственное решение. Такой вариант нас не устраивает, поэтому будем рассматривать все 
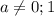. Для них квадратное уравнение имеет два корня:
Чтобы исходное уравнение имело два корня необходимо, чтобы оба корня удовлетворяли ОДЗ, т.е.
Не забудем исключить 0 и 1 из данного промежутка значений и получим окончательный ответ.
ОТВЕТ: при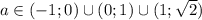
.