


Пусть  Тогда
Тогда 

Имеем дифференциальное уравнение, однородное относительно переменных.
Подстановка:  где
где 
Имеем:











Обратная подстановка:




ответ: 
а)8 5/7+3,15+1 2/7+4,25=(8 5/7+1 2/7)+(3,15+4,25)=10+7,4=17,4
б)4,7+2/3+1 3/5+3,3=(4,7+3,3)+(2/3+1 3/5)=8+2 4/15=10 4/15
в)8 19/20+5,875+20 35/40=(8 19/20+20 35/40)+5,875=29 33/40+5,875=29 33/40+5 35/40=34 68/40=34 17/10=35,7
г)6,75+3 1/4-7 5/28=(3 1/4-7 5/28)+6,75= -3 13/14+6,75= -3 13/14+6 3/4=2 23/28
д)2,1+1 7/30-(4-2,9)=2,1+1 7/30-1,1=(2,1-1,1)+1 7/30=1+1 7/30=2 7/30
е)22-(4 5/7+8,91+1,09)=22-(4 5/7+10)=22-4 5/7-10=(22-10)-4 5/7=12-4 5/7=7 2/7
ж)76-4 7/25+8,28=(76+8,28)-4 7/25=84,28-4 7/25=84 7/25-4 7/25=80
з)2 5/6-1,6-2/3=(2 5/6-2/3)-1,6=2 1/6-1,6=17/30
9 м²
Пошаговое объяснение:
Смотри рисунок
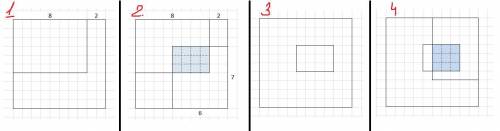
ШАГ 1.
Рисуем "актовый зал" - квадрат 10х10. Заметим, длина 1 клеточки - 1 м.
В квадрате рисуем первый ковёр 6×8.
ШАГ 2.
Рисуем второй ковёр 6×7. И находим часть зала, которая накрыта и первым и вторым ковром.
ШАГ 3.
Рисуем "актовый зал" - квадрат 10х10. И рисуем часть зала, которая накрыта и первым и вторым ковром.
ШАГ 4.
Рисуем третий ковёр 5×7. И находим часть зала, которая накрыта в три слоя (первым и вторым и третьим ковром).
Это квадрат 3х3 (3м х 3м).
ШАГ 5.
Найдем площадь квадрата.
 (м²)
(м²)

решение на фотографии