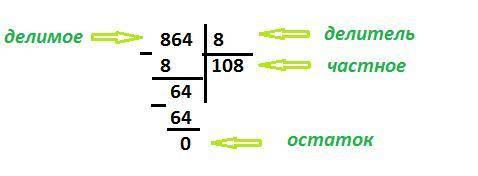
1) Первая цифра 8 делится на 8 нацело, записываем в частное 1.
1 · 8 = 8 → записываем под старшей 8 в числе 864 и вычитаем.
8 - 8 = 0
2) Сносим вниз следующую цифру 6 из числа 864. 6 < 8, на 8 поделить нельзя. Записываем в частное 0.
3) Сносим вниз следующую цифру 4 из числа 864. 64 делится на 8 нацело. Записываем в частное 8.
8 · 8 = 64 → записываем под числом 64 и вычитаем.
64 - 64 = 0
Все цифры числа 864 снесены вниз и поделены, деление закончено. Остаток равен нулю. Частное равно 108.
864 : 8 = 108
Решение .
Предположим, что шестиугольник только один. Тогда количество вершин у пятиугольников равно 28 - 6 = 22. Этого не может быть, потому что число 22 на 5 не делится.
Если шестиугольник два, то количество вершин у пятиугольников равно 28 - 12 = 16, чего не может быть.
Если шестиугольник три, то количество вершин у пятиугольников равно 28 - 18 = 10. Значит, пятиугольников может быть два.
Если шестиугольников четыре, то количество вершин у пятиугольников равно 28 - 24 = 4, чего не может быть.
Больше четырех шестиугольников быть не может.
если что это 6 класс если не то скажи
Пошаговое объяснение:
если что это 6 класс если не то скажи
всал со сайта vcevce