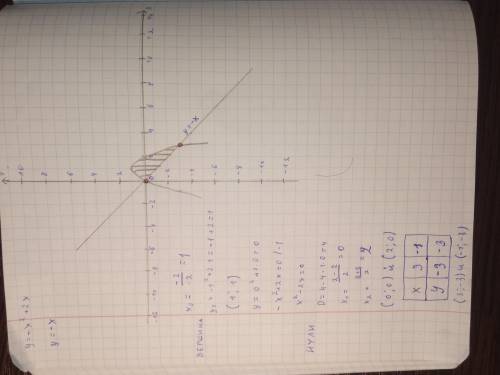
Сперва рисуем два графика и находим фигуру, которая появляется при их пересечении. Как мы это сделали - смотри на фото.
Число 0 будет нижним пределом интегрирования (ибо самая "левая" точка пересечения графиков (0; 0) (смотрим по х) ), а 3 - верхним (ибо самая "самая" правая точка пересечения - (3;-3), опять же, смотрим по х).
Дальше приравняем две функции:
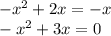
Теперь площадь фигуры можно найти через определённый интеграл:
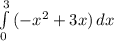
Найдём для начала неопределённый интеграл:
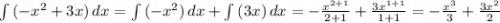
Теперь подставим пределы интегрирования:
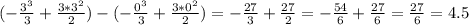
S = 4.5
10 чисел
Пошаговое объяснение:
Наибольшее количество единиц в своей двоичной записи имеют числа вида 2^n - 1, при n - натуральное число.
Соответственно:
2^1 - 1 = 1
2^2 - 1 = 3
2^3 - 1 = 7
2^4 - 1 = 15
2^5 - 1 = 31
2^6 - 1 = 63
2^7 - 1 = 127
2^8 - 1 = 255
2^9 - 1 = 511
2^10 - 1 = 1023
2^11 - 1 = 2047 - Тут мы получили число, превосходящее 2020, значит ответ - все идущие до него
ответ: 10 чисел