

2) 32 га;
3) 6480 см3
4) 330
5) 69 см2
Пошаговое обьяснение:
2) 500 м - ширина
500+140=640 м - длина
S=ширина*длину
S=500*640=320000 м2:10000=32 га
3) 12 см - ширина
12*3=36 см - длина
12+3=15 см - высота
V=ширина*длину*высоту
V=12*36*15=180*36=6480 см3
4) 1) 15600:65=240
2) 240*86=20640
3) 20640+240=20880
4) 20880-20550=330
5) 23 см - ширина
х - длина, если длину увеличить на 3,
(х+3) - новая длина.
S1=23*x
S2=23*(x+3)=23x+69=S1+69, следовательно с увеличением длины на 3 см, площадь прямоугольника увеличится на 69 см2.
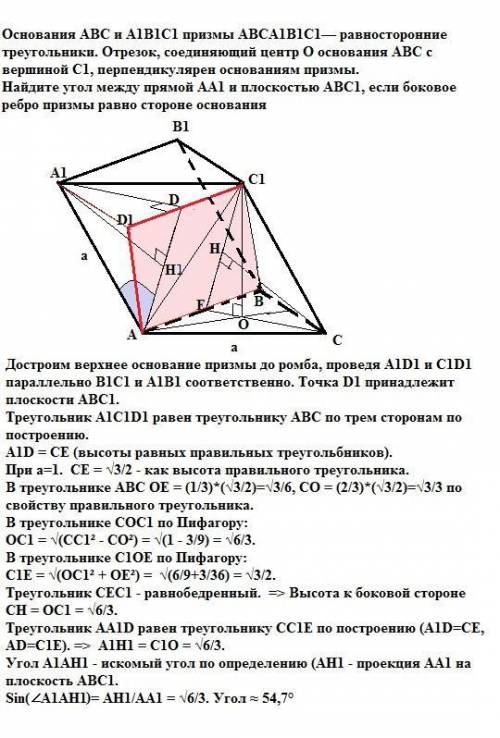
Угол между прямой AA1 и плоскостью ABC1 равен
arcsin(√6/3). Угол ≈ 54,7°
Пошаговое объяснение:
Достроим верхнее основание призмы до ромба, проведя A1D1 и C1D1 параллельно B1C1 и A1B1 соответственно. Точка D1 принадлежит плоскости АВС1.
Треугольник А1С1D1 равен треугольнику АВС по трем сторонам по построению.
A1D = CE (высоты равных правильных треугольбников).
При а=1. CE = √3/2 - как высота правильного треугольника.
В треугольнике АВС ОЕ = (1/3)*(√3/2)=√3/6, СО = (2/3)*(√3/2)=√3/3 по свойству правильного треугольника.
В треугольнике СОС1 по Пифагору:
ОС1 = √(СС1² - СО²) = √(1 - 3/9) = √6/3.
В треугольнике С1ОЕ по Пифагору:
С1Е = √(ОС1² + ОЕ²) = √(6/9+3/36) = √3/2.
Треугольник CEC1 - равнобедренный. => Высота к боковой стороне СН = ОС1 = √6/3.
Треугольник АА1D равен треугольнику СС1Е по построению (A1D=CE, AD=C1E). => A1H1 = C1O = √6/3.
Угол A1АН1 - искомый угол по определению (AH1 - проекция АА1 на плоскость АВС1.
Sin(∠A1AH1 = AH1/AA1 = √6/3. Угол ≈ 54,7°
29854400...
Пошаговое объяснение: