Question

Если линия имеет точки A (-2; 2) и B (5; -3), то уравнение прямой имеет вид

Answer 1

Пошаговое объяснение:

Общее уравнение прямой на плоскости:

$ax+by+c=0$

Прямая должна проходить через точки A (-2,2) и B (5,-3), т.е.:

$A: a(-2)+2b+c=0\\B: 5a+(-3)b+c = 0$

Получили систему уравнений:

$\left \{ {{a(-2)+2b+c=0} \atop {5a+(-3)b+c = 0}} \right.$

Домножим первое уравнение на 3, второе на 2 и сложим:

$\left \{ {{-6a+6b+3c=0} \atop {10a-6b+2c = 0}} \right.\\4a+5c = 0$

откуда $a=-\frac{5}{4}c$

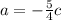
Подставим a во второе уравнение:

$5(-\frac{5}{4}c)+(-3)b+c = 0\\-\frac{25}{4}c-3b+c = 0\\-\frac{21}{4}c-3b = 0\\-3b = \frac{21}{4}c\\b=- \frac{7}{4}c$

Подставим a и b в уравнение прямой:

$-\frac{5}{4}cx+( -\frac{7}{4}c)y+c=0$

Делим на c и домножаем на 4, получаем:

$-5x-7y+4=0$

Проверка:

Для точки A: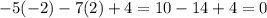 $-5(-2)-7(2)+4 = 10-14+4=0$ (верно)

Для точки B: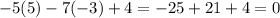 $-5(5)-7(-3)+4 = -25+21+4=0$ (верно)