Математика: 5log2x=3log2x+6 2 внизу ln3+1/2 ln5 +1/2ln=ln6

Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида Если a 0, это сразу дает два решения если a 0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что...

5log2x=3log2x+6 2 внизу ln3+1/2 ln5 +1/2ln=ln6

👇

Увидеть ответ

Ответ:

автормемовв

27.05.2020

5log2x-3log2x=6

log2x^5-log2x^3=6

log2(x^5/x^3)=6

log2x^2=log2 64

x^2=64

x=8 и х=-8 - не удовлетворяет ОДЗ, ответ х=8

ln3+1/2 ln5 +1/2ln=ln6 - условие проверь, 1/2ln - ?

4,5(53 оценок)

Открыть все ответы

Ответ:

poulina14

27.05.2020

1. Опасное природное явление - событие природного происхождения или состояние элементов природной среды, которые по своей интенсивности, масштабу распространения и продолжительности могут вызвать поражающее воздействие на людей, объекты экономики и окружающую среду.

2. Природные явления - это дождь, облака. цунами. Стихийные бедствия - землетрясения, ураганы, лавины, лесные пожары.

3. Землетрясения, наводнения, ураганы.

4. Россия, имеющая чрезвычайно большое разнообразие геологических, климатических и ландшафтных условий, подвержена воздействию более 30 видов опасных природных явлений. Наиболее разрушительными из них являются наводнения, подтопления, эрозия, землетрясения, оползни, сели, карсты, суффозии, горные удары, снежные лавины, ураганы, штормовые ветры, смерчи, сильные заморозки, различные мерзлотные явления. Наибольшую опасность представляют собой землетрясения. Только за последние годы на территории Российской Федерации произошло более 120 землетрясений. Два из них – на Курилах 4 октября 1994 г. и в пос. Нефтегорск 27 мая 1995 г. были очень сильными и привели к человеческим жертвам, сильным разрушениям объектов социальной и промышленной инфраструктуры в эпицентральных районах, а также к разрывам, трещинам, оползням и другим деформациям земной поверхности.

4,4(78 оценок)

Ответ:

viliam3486

27.05.2020

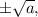Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида x^2-a. Если a>0, это сразу дает два решения $\pm \sqrt{a},$ если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида 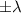$\pm \lambda$ я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни 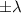$\pm\lambda$ тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна 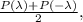$\frac {P(\lambda)+P(-\lambda)}{2},$ а сумма нечетных равна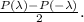 $\frac{P(\lambda)-P(-\lambda)}{2}.$

Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.

1) Разбиваем на четные и нечетные степени: $x^6+2x^4-5x^2-6=t^3+2t^2-5t-6=0\ \ (t=x^2);$

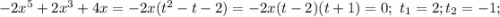
$-2x^5+2x^3+4x=-2x(t^2-t-2)=-2x(t-2)(t+1)=0;\ t_1=2; t_2=-1;$

найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем

(t-2)(t+1)(t+3)-2x(t-2)(t+1)=0; (t-2)(t+1)(t-2x+3)=0; (x²-2)(x²+1)(x²-2x+3)=0.

ответ: $\pm\sqrt{2}.$