Задание #2 Вам предстоит разгадать задачу.
5 героев - Азула, Айро, Аанг, Катара и Зуко - поехали за подарками на праздник со своим друзьям.
Один из них купил шапку, второй - горшок, третий - чай, четвертый - шарф, а пятый - картину. Каждый потратил определённую сумму: один - 60 золота, второй - 230 золота, третий - 200 золота, четвертый - 160 золота и пятый - 140 золота.
Подарки были куплены для: Тоф , Сокки, Буми, Аппы и Момо.
Определите кто кому купил какой подарок и сколько золота потратил, если:
1. Картину купил не Аанг
2. Герой который купил шапку заплатил 140 золота.
3. На подарок Сокки потратили 160 золота, но это был не шарф и не горшок.
4. Айро потратил на подарок Момо золота больше чем было потрачено на подарок Буми
5. Чай купили Тоф. На этот подарок потратили больше, чем потратили Аанг и Катара.
6. 60 золота потратил Зуко но не на горшок и покупал он подарок не Тоф и не Аппе.взведемо храм видродження
Это следует из свойства выражения с модулем иметь 2 значения - положительное и отрицательное.
Если раскрыть модуль, то получаем 2 функции:
- при положительном значении модуля
- при положительном значении модуля
у = х² - 2х,
- при отрицательном значении модуля
у = -х² - 4х.
Границей является ось у, делящая ось х на положительные и отрицательные значения.
Находим вершины парабол:
у = х² - 2х хо = -в/2а = -(-2)/2*1 = 2/2 = 1,
уо = 1² - 2*1 = 1-2 = -1.
у = -х² - 4х хо = -в/2а = -(-4/2*(-1) = 4/-2 = -2,
уо = -(-2)² - 4*(-2) = -4 +8 = 4.
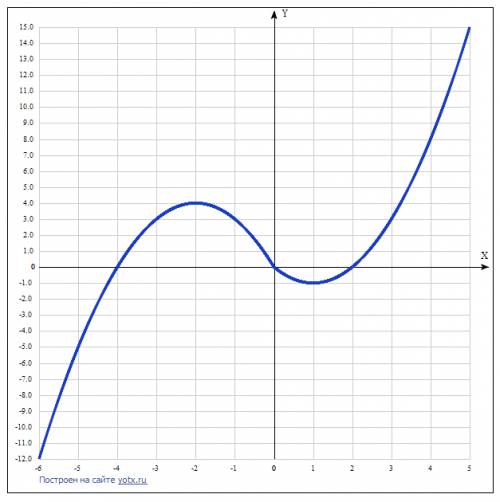
Прямая y = m может иметь только 2 точки с графиком заданной функции - это прямая, касательная к вершинам парабол.
Таких прямых 2:
у = -1,
у = 4.
График и таблица координат точек для его построения приведены в приложениях.